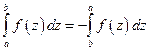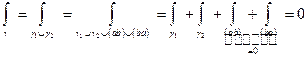Формула Грина
Интегрирование функций комплексного переменного.
Особые точки аналитических функций
1) полюс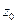 
: 
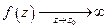
- полюс для 
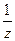
2) существенно особые точки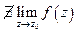 
3) точки ветвления
для 
, 
.
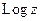Интеграл от функции комплексного переменного по пути (кривой) определяется как обычный криволинейный интеграл II рода.
,
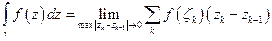где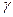 
- кривая.
,
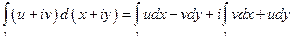т.е. криволинейные интегралы II рода.
Пример: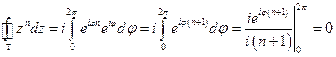 
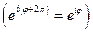при 
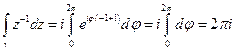
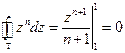
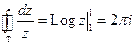
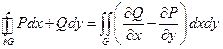
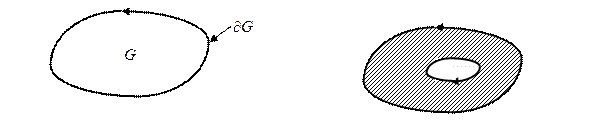
Если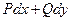 
- полный дифференциал некоторой функции двух переменных
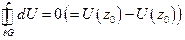
(интеграл по любому замкнутому контуру = 0)
,
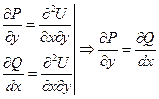
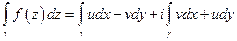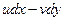- полный дифференциал, CR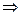
,
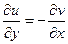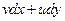- полный дифференциал, CR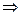
.
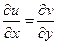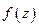- аналитична
1) 
2) Первообразная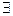 
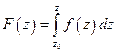
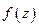аналитична в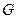 
разрез 
