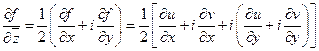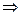- поле комплексных чисел
, 
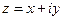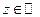базис 
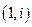
- вектор в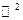 
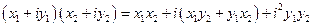
Можно положить 
Стандартная система комплексных чисел будет при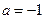 
, 
.
Функция комплексного переменного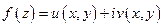 
, 
, .
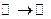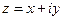Опр.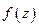 
называется дифференцируемой (аналитической) (в т. 
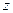), если существует
.
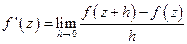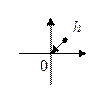Предел должен существовать вдоль любого направления. 
1) 
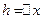
2) 
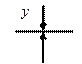
1) 
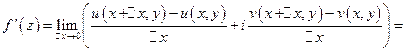
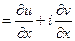
2) 
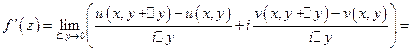
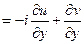
Приравниваем производные, получим 
- уравнения Коши-Римана
и наоборот, если выполняются условия Коши-Римана, то функция дифференцируемая.
В последнем случае существуют полные дифференциалы
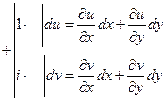
Существует полный дифференциал функции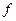 
: 
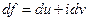
Введем обозначение:
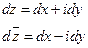
Частные производные
,
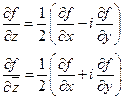которые имеют смысл, даже если 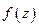не дифференцируема, а функци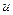и 
и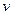 
дифференцируемы.
Тогда
Если же 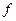дифференцируема (т.е. выполняется условие Коши-Римана), то 
