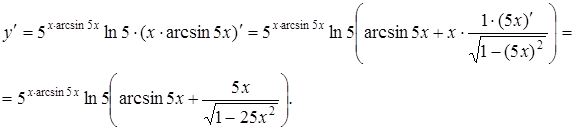Основные правила дифференцирования
Пусть функция 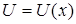 и
и 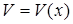 имеют производные в любой точке их области определения
имеют производные в любой точке их области определения 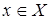 .
.
1. 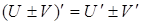 ; (5.4)
; (5.4)
2. 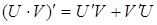 ; (5.5)
; (5.5)
3.  , (5.6)
, (5.6)
где С = const;
4. 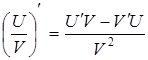 . (5.7)
. (5.7)
5. Производная сложной функции.
Пусть задана сложная функция: 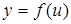 , где
, где 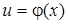 , т.е.
, т.е.
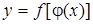 . (5.8)
. (5.8)
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.
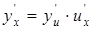 . (5.9)
. (5.9)
6. Производная обратной функции.
Пусть функция 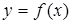 имеет однозначную обратную функцию
имеет однозначную обратную функцию 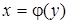 , непрерывную при
, непрерывную при 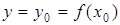 , тогда при
, тогда при 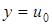 существует производная обратной функции
существует производная обратной функции
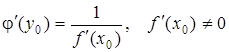 или
или 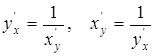 . (5.10)
. (5.10)
Пример 1. 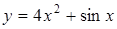 .
.
Решение. Применим формулу (5.4);
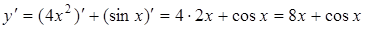 .
.
Пример 2. 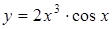 .
.
Решение. Применим формулу (5.5);
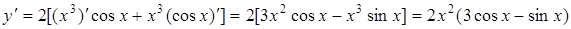 .
.
Пример 3. 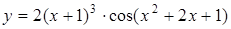 .
.
Решение. Данная функция является сложной. Если ввести промежуточный аргумент для функций 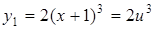 , где
, где 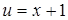 и
и  , где
, где  , то производная с учетом формул (5.5) и (5.9) примет вид
, то производная с учетом формул (5.5) и (5.9) примет вид
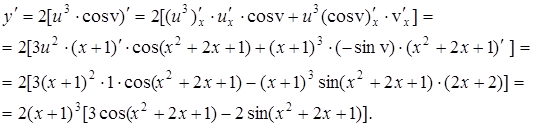
Таблица 5
| Простая функция
| Сложная функция
|
|
|
|
1. 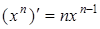
| 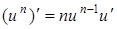
|
3. 
| 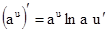
|
4. 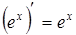
| 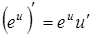
|
5. 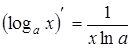
| 
|
6. 
| 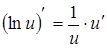
|
7. 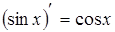
| 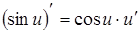
|
8. 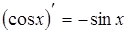
| 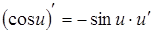
|
9. 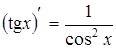
| 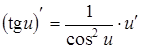
|
10. 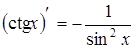
| 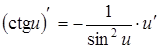
|
11. 
| 
|
12. 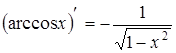
| 
|
13. 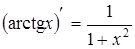
| 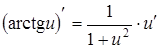
|
14. 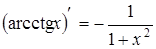
| 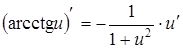
|
15. 
| 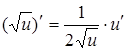
|
16. 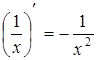
| 
|
Пример 4.  .
.
Решение. Это сложная функция с промежуточным аргументом 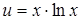 , т.е.
, т.е. 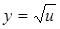 ;
;
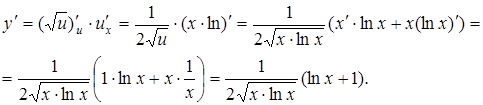
Пример 5. 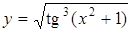 .
.
Решение. Данная функция является сложной. Представим 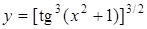 с промежуточным аргументом
с промежуточным аргументом 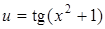 , который сам является сложной функцией с промежуточным аргументом
, который сам является сложной функцией с промежуточным аргументом 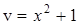 , т.е.
, т.е. 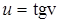 . Тогда
. Тогда 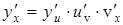 . Действительно,
. Действительно,
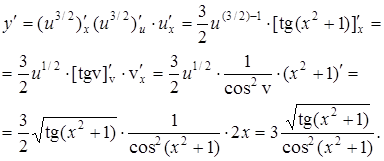
Пример 6. 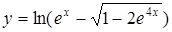 .
.
Решение:
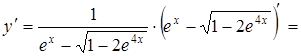
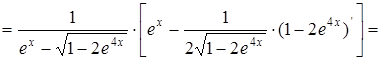

Пример 7. 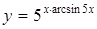 .
.
Решение: