Пусть дана функция 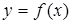 (рис. 76),
(рис. 76), 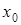 - фиксированная точка. Проведем в точке
- фиксированная точка. Проведем в точке 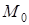 касательную
касательную 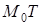 к графику функции
к графику функции 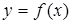 , которая составляет с осью ОХ угол a.
, которая составляет с осью ОХ угол a.
 Рис. 76
Рис. 76
| Проведем секущую 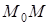 . Найдем отношение . Найдем отношение 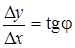 . При стремлении . При стремлении 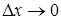 точка точка 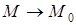 , секущая , секущая 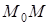 будет стремиться занять положение касательной будет стремиться занять положение касательной 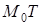 , тогда , тогда 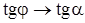 : :
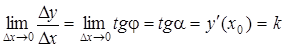 . .
|
В ы в о д: значение производной, вычисленной в данной точке (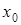 ,
, 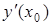 ), есть угловой коэффициент касательной, проведенной к графику функции в данной точке
), есть угловой коэффициент касательной, проведенной к графику функции в данной точке 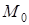 :
:
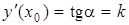 .
.
Уравнение касательной к 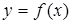 в точке
в точке 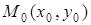
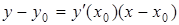 . (5.3)
. (5.3)
Пример 2. Найти уравнение касательной к кривой, заданной уравнением 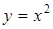 , в точке
, в точке  .
.
Решение. Найдем  , тогда
, тогда
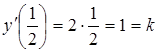 .
.
Уравнение касательной 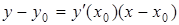 примет вид
примет вид
 .
.
Ответ: 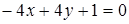 .
.
П р и м е ч а н и е. 1. Дифференцируемость функции в точке с геометрической точки зрения означает, что к графику функции в данной точке можно провести единственную невертикальную касательную.
2. Если функция недифференцируема в точке, то это означает, что касательная к графику функции в точке проходит вертикально  . В данной точке к графику функции можно провести больше, чем одну касательную (рис. 77).
. В данной точке к графику функции можно провести больше, чем одну касательную (рис. 77).

| 
|
| Рис. 77
|
3. Физический смысл производной функции в точке есть скорость изменения функции в данной точке.