Классификация точек разрыва
О п р е д е л е н и е 1. Точкой разрыва первого рода функции 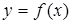 называется такая точка
называется такая точка 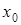 , в которой функция имеет левый и правый пределы, неравные между собой (рис. 69).
, в которой функция имеет левый и правый пределы, неравные между собой (рис. 69).
 Рис. 69
Рис. 69
|
 (4.32) (4.32)
|
О п р е д е л е н и е 2. Точка 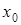 (рис. 70) называется точкой разрыва второго рода функции
(рис. 70) называется точкой разрыва второго рода функции 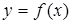 , если хотя бы один из односторонних пределов не существует или равен бесконечности:
, если хотя бы один из односторонних пределов не существует или равен бесконечности:
 и
и 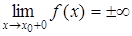 . (4.33)
. (4.33)
О п р е д е л е н и е 3. Точка 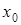 (рис. 71) называется точкой устранимого разрыва
(рис. 71) называется точкой устранимого разрыва 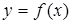 , если функция в точке неопределена, но односторонние пределы существуют и равны между собой:
, если функция в точке неопределена, но односторонние пределы существуют и равны между собой:
 , но
, но 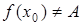 . (4.34)
. (4.34)
Такой разрыв можно устранить, доопределив функцию в точке разрыва 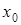 значением ее предела А:
значением ее предела А:
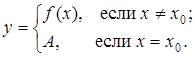
Пример. Исследовать функцию на непрерывность, выявить точки разрыва и определить их типы:
1) 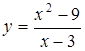 ; 2)
; 2) 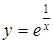 ; 3)
; 3)  .
.
Решение:
1) 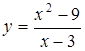 . Данная функция определена на всей числовой оси за исключением точки
. Данная функция определена на всей числовой оси за исключением точки  .
.  , т.е.
, т.е.  является точкой разрыва. Определим тип разрыва:
является точкой разрыва. Определим тип разрыва:
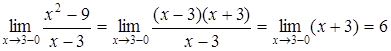 ,
,
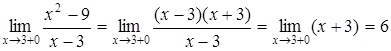 ,
,
т.е. 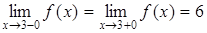 , но
, но 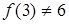 . Таким образом, имеет место точка устранимого разрыва. Чтобы устранить разрыв, положим значение функции в точке
. Таким образом, имеет место точка устранимого разрыва. Чтобы устранить разрыв, положим значение функции в точке 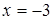 равным значению односторонних пределов:
равным значению односторонних пределов:
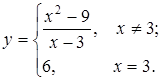 - функция является непрерывной.
- функция является непрерывной.
2) 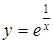 . Область определения
. Область определения 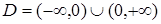 ,
, 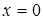 - точка разрыва. Исследуем на тип разрыва:
- точка разрыва. Исследуем на тип разрыва:
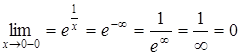 , ,
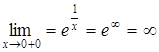 . . 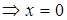 - точка разрыва 2-го рода (рис. 73).
Найдем - точка разрыва 2-го рода (рис. 73).
Найдем 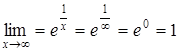 . .
| 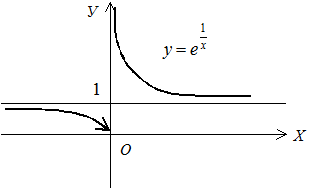 Рис. 73
Рис. 73
|
3)  . Область определения
. Область определения 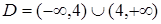 ,
, 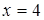 - точка разрыва. Исследуем на тип разрыва:
- точка разрыва. Исследуем на тип разрыва:
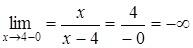 , ,
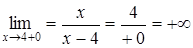 ; ;
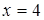 - точка разрыва 2-го типа
(рис. 74).
Найдем - точка разрыва 2-го типа
(рис. 74).
Найдем 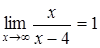 . .
|  Рис. 74
Рис. 74
|