Эквивалентные бесконечно малые величины
Пусть даны две бесконечно малые величины 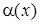 и
и 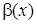 при
при 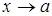 ,
,
 и
и 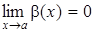 .
.
Чтобы сравнить две бесконечно малые величины, нужно найти предел их отношения.
О п р е д е л е н и е. Бесконечно малые величины 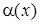 и
и 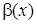 называются эквивалентными, если предел их отношения равен единице:
называются эквивалентными, если предел их отношения равен единице:
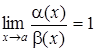 .
.
Обозначается 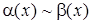 .
.
Пример 1.  .
.
Действительно, 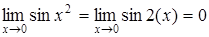 , где
, где 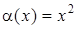 ,
, 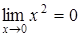 ,
, 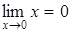 , т. е. при
, т. е. при 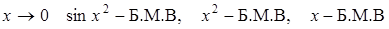 .
.
Т е о р е м а. Предел отношения двух бесконечно малых величин равен пределу отношения эквивалентных им бесконечно малых величин.
Данная теорема используется при раскрытии неопределенности вида 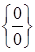 . Эквивалентные бесконечно малые величины приведены в табл. 4, где
. Эквивалентные бесконечно малые величины приведены в табл. 4, где  .
.
Таблица 4
| 1.
| 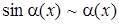
| 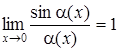
|
| 2.
| 
| 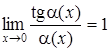
|
| 3.
| 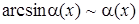
| 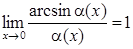
|
| 4.
| 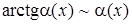
| 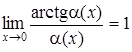
|
| 5.
| 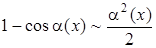
| 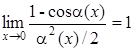
|
| 6.
| 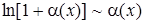
| 
|
| 7.
| 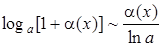
| 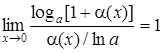
|
| 8.
| 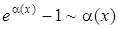
| 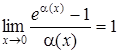
|
| 9.
| 
| 
|
| 10.
| 
| 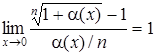
|
Пример 2.  ,
,
так как 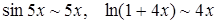 .
.
Пример 3. ,
,
так как 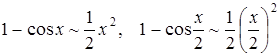 .
.
Пример 4.  ,
,
так как 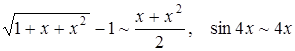 .
.
4.9. Раскрытие неопределенностей 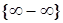 и
и 
П р а в и л о 1. Если при вычислении предела, представляющего собой разность двух функций, получим неопределенность 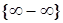 , то чтобы избавиться от неопределенности, надо, или привести функции к общему знаменателю, или, при наличии иррациональности, перенести ее из числителя в знаменатель.
, то чтобы избавиться от неопределенности, надо, или привести функции к общему знаменателю, или, при наличии иррациональности, перенести ее из числителя в знаменатель.