Максимизация первого столбца

Метод максимизации столбцов

Пусть A=(a_kp) – вещственная, квадратная матрица порядка n.

Обозначим как a_p – pый столбец матрицы.

Заметим, что ; .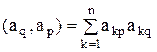

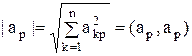Рассмотрим матрицу простого поворота U_p:

u₁₁ = u_pp= c =cosα, -u_p1 = u_1p= -s = - sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Из ранее доказанного матрица U_p осуществляет поворот на угол α против часовой стрелки.

Рассмотрим матрицу B=AU_p=(b_ij).

В ней: b₁ = ca₁+sa_p, b_p = -sa₁+ca_p. Остальные столбцы совпадают со столбцами А.

Свойство 1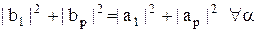

Доказательство

Действительно:

.

Отсюда .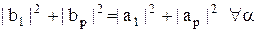

Что и требовалось доказать.

Выберем угол α в матрице U_p так, чтобы | b₁ | был максимален.

Рассмотрим функцию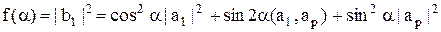

Тогда .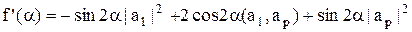

Обозначим α=α_p: f ’(α)=0. Будем выбирать α_p по правилу:

а)если 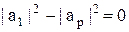, то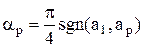

б)иначе α_p находится из равенства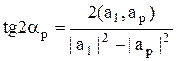

в) заметим, что α_p=0 тогда и только тогда, когда .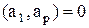

Свойство 2Если | a₁|≥| a_p|, то | b₁|≥| a₁|≥| a_p|≥| b_p| и | b₁|>| a₁| при .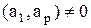

Доказательство

Действительно:

1) Пусть 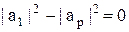. Тогда 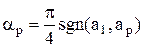и .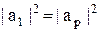

Следовательно, из определения f(α): .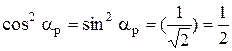

Отсюда:

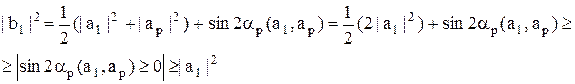
и | b₁|>| a₁| при .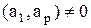

2) Пусть .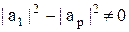

Рассмотрим функцию .

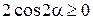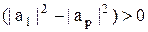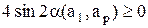Т.к. , , a , то

f ’’(α_p)≤0, т.е. α_p – локальный максимум (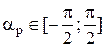) и общий максимум функции на .

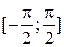Следовательно, .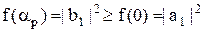

Что и требовалось доказать.

Свойство 3 Если | a₁|≥| a_p|, то 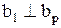, т.е. новые столбцы ортогональны.

Доказательство

Действительно:

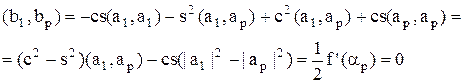
Что и требовалось доказать.