Интерполяционный полином в форме Лагранжа
Из системы (2) получим систему следующего вида:
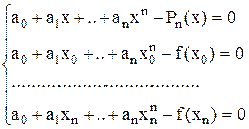(3)
Будем считать неизвестными a0,a1..an , -1.
Полученная система имеет (n+1) порядок. Ее нетривиальное решение из предыдущей теоремы существует, следовательно, ее определитель равен 0 (иначе решение (3) было бы нулевым).
Разложим этот определитель по последнему столбцу:
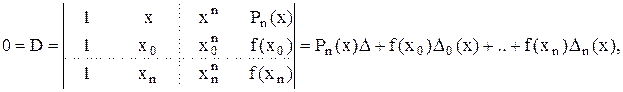
где 
- многочлены n-ой степени,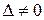 
.
Перпишем последнее равенство в ви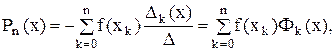де:
где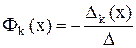 
.
Заметим, что:
1) 
- многочлен n-ой степени
2) 
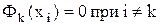
3) 
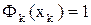
Следовательно, многочлен определяется единственным образом.
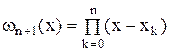
Рассмотрим следующий многочлен (n+1)ой степени:
Обозначим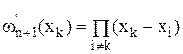 
.
Заметим, что:
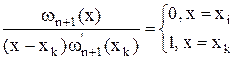
Т.о. =
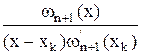, т.е. интерполяционный полином имеет вид:
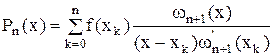- интерполяционный полином Лагранжа
Представим функцию f(x) в виде: f(x)=Pn(x)+Rn(x), где Rn(x) – погрешность интерполяции. Заметим, что Rn(x) зависит от свойств f(x) (так если f(x) линейна, то Rn(x)≡0 при n>2).
Будем считать априорно, что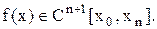 
а
Запишем погрешность в виде: Rn(x)=kωn+1(x)+φ(x).
Тогда φ(x)=f(x)-Pn(x)- kωn+1(x) и φ(xk)=0,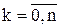 
. (4)
Выберем k из условия φ(x’)=0, где x’ – точка, в которой оценивается погрешность: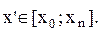 
Из уравнения φ(x’)=0 получим: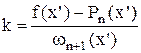 
.
При таком выборе k φ(x’)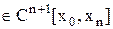
и обращается в ноль в (n+2) точках: x0…xn,x’.
Тогда по т. Ролля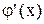 
обращается в ноль в по крайней мере (n+1) точке. И т.д.
По т. Ролля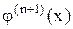 
имеет хотя бы один нуль. Т.е.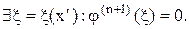 
Т.о. из (4) получим:
.
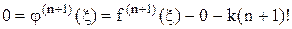Тогда 
, а значит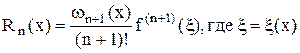 
, т.к. точка x’ была выбрана произвольно.
