Определение 12.6. Функция 
называется бесконечно малой в точке 
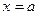(при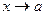 
), если 
.
Например, 
, где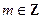 
, – бесконечно малая функция в любой точке 
, в силу утверждения 12.3:
.
☼ Замечание 12.3. Если 
, то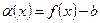 
– бесконечно малая в точке a. Отсюда следует специальное представление функции 
, где 
. Говорят, что функция 
асимптотически равна b при . ☼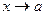
Определение 12.7. Функция называется бесконечно большой в точке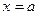справа (слева), если для любой последовательности 
: 
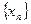при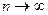 
, 
(
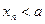), соответствующая последовательность 
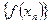значений функции является бесконечно большой последовательностью определённого знака.
Например, функция 
является бесконечно большой при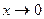 
, 
.
Возможны ситуации и для случая односторонних пределов:
; 
.
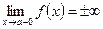Рассмотрим функцию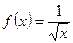 
вблизи точки 
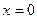. Так как она определена лишь при 
, то вблизи 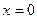её можно исследовать только при 
: 
. То есть функция 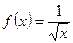– положительная бесконечно большая при .
