Арифметические операции над функциями, имеющими предел в точке a, приводят к функциям, также имеющим предел в точке a.
♦ Теорема 12.2.Пусть две функции 
и 
заданы на одном и том же множестве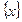 
и имеют в точке a пределы, равные b и c. Тогда
,
,
.
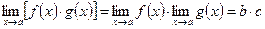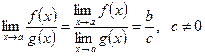Доказательство.Пусть 
– произвольная, сходящаяся к а последовательность значений аргумента функций и . Соответствующие последовательности 
и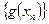 
значений этих функций имеют пределы b и c. Но тогда, в силу теорем 9.3-9.5, последовательности 
, 
и 
при 
имеют пределы, соответственно равные 
, 
и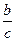 
. Согласно определению 12.1 предела функции, это означает, что 
, 
, 
. ■
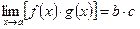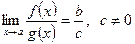♦ Утверждение 12.3. Многочлен степени n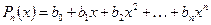 
, где 
, имеет предел в любой точке 
, причём этот предел 
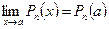равен частному значению многочлена в точке a.
Доказательство:Так как 
, 
, то 
и .■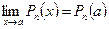
♦ Утверждение 12.4. Рациональная дробь (частное 
) имеет предел в любой точке , не являющейся корнем её знаменателя 
, причём
.
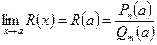