Б. Четность и нечетность.
А. Монотонность.
Свойства функции.
Функции одной действительной переменной
Определение I.4. Пусть X и Y – два числовых множества и пусть каждому элементу x множества X поставлен в соответствие единственный элемент y из множества Y. Тогда говорят, что задана функция, определенная на множестве X со значениями в множестве Y и пишут 
. X называют областью определения функции 
, а областью значений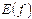 
называют множество тех элементов из Y, которые участвуют в соответствии: 
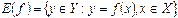. При этом x называют независимой переменной или аргументом, а 
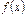– значением функции f в точке x.
Определение I.5.1. Функция f называется строго возрастающей на множестве Х, если для любых двух значений аргумента x1 и x2, взятых из этого множества, неравенство 
влечет за собой 
. В случае нестрогого неравенства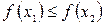 
функцию называют возрастающей нестрого или возрастающей в широком смысле.
f строго возрастает на X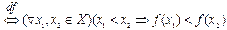 
.
Определение I.5.2. f строго убывает на X 
. В случае неравенства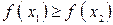 
функция f называетсяубывающей нестрого.
Определение I.5.3. Функция f называется монотонной на множестве Х, если она на Х возрастает или убывает. Монотонность тоже бывает строгая или нестрогая.
Определение I.5.4. Функция f называется четной, если для любого 
выполняются два условия: 1. 
; 2. 
Определение I.5.5. f нечетная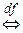 
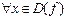1. 
и 2. 
.
Определение I.5.6. Функция f называется периодической, если существует такое число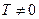 
, что для любого 
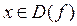выполняются два условия:
1)
если 
, то и 
; 2)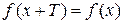 
.
