Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.
Каноническое уравнение эллипса:
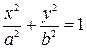. (2)
Так как уравнение (2) содержит только квадраты текущих координат, то если точка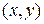 
находится на эллипсе, то и точки 
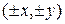находятся на эллипсе при произвольном выборе знаков у координат; следовательно, оси координат являются осями симметрии эллипса.
Полагая в уравнении (2)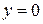 
, можно найти абсциссы точек пересечения эллипса с осью Ох: 
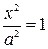, откуда 
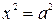и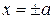 
.
Полагая в уравнении (2)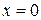 
, можно найти ординаты точек пересечения эллипса с осью Оу: 
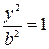, откуда 
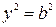и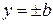 
.
Следовательно, вершинами эллипса будут точки:
, 
, 
, 
.
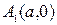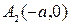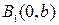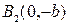