Общее уравнение второй степени относительно переменных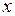 
и 
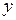может содержать члены второй степени (
, 
, 
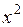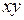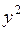), первой степен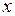и (и 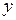) и нулевой степени (свободный член): 
.
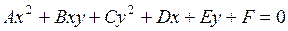Здесь по крайней мере один из коэффициентов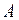 
, 
, 
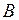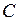должен быть отличен от нуля.
Окружность с центром в точке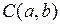 
и радиусом 
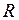имеет уравнение
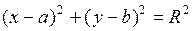. (1)
Раскрывая скобки, придадим уравнению (1) вид:
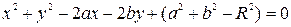, (1′)
или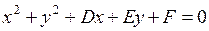 
, (1′′)
где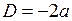 
, 
, 
.
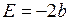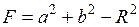Уравнение окружности (1′′) является уравнением второй степени. Но, очевидно, не всякое уравнение второй степени определяет окружность. Действительно, из уравнения (1′′) видно, что в уравнении окружности коэффициенты при квадратах координат равны, а член с произведением координат (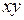) отсутствует.
