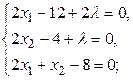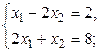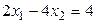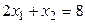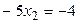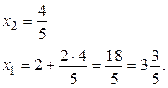ОДР ограничена прямыми 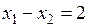 ,
, 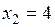 , осями координат
, осями координат 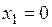 ,
, 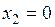 и гиперболой
и гиперболой 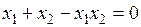 , уравнение которой приводится к виду
, уравнение которой приводится к виду 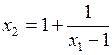 .
.
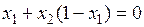 ,
, 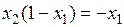 ,
, 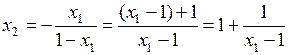 .
.
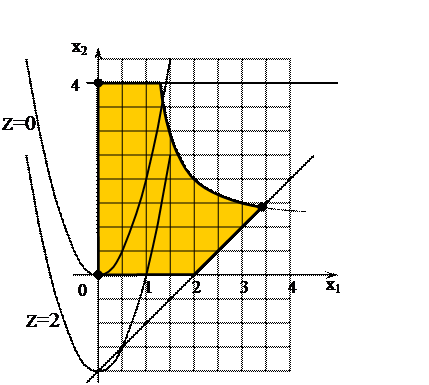
Линии уровня целевой функции: 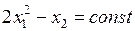 . Для разных значений
. Для разных значений 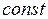 графиком уравнения
графиком уравнения 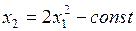 является парабола с осью симметрии
является парабола с осью симметрии 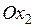 .
.
При 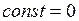 парабола проходит через начало координат.
парабола проходит через начало координат.
При 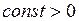 параболы сдвигаются вниз.
параболы сдвигаются вниз.
Перемещая целевую функцию в направлении возрастания, получим, что максимум 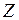 достигается на пересечении гиперболы и прямой
достигается на пересечении гиперболы и прямой 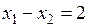 . Решая систему, составленную из этих двух уравнений, найдём координаты точки пересечения:
. Решая систему, составленную из этих двух уравнений, найдём координаты точки пересечения:
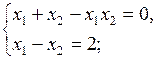
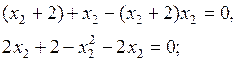
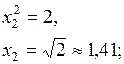
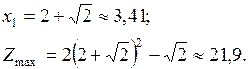
Минимум функции 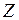 достигается в точке
достигается в точке 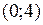 .
.
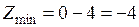 .
.
Вариант 18.Метод множителей Лагранжа.
Задача а) Найти точку условного экстремума функции 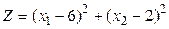
при ограничении 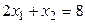 .
.
Решение.
1) Составление функции Лагранжа.
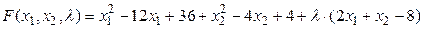 , где
, где 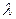 - множитель Лагранжа.
- множитель Лагранжа.
2) Дифференцирование функции 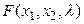 по переменным
по переменным 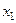 ,
, 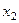 и
и 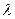 .
.
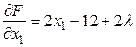 ,
, 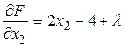 ,
, 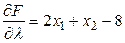 .
.
3)  Составление системы уравнений (для этого полученные выражения частных производных приравнивают к нулю) и решение её.
Составление системы уравнений (для этого полученные выражения частных производных приравнивают к нулю) и решение её.