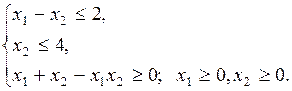Решение.

Уравнение 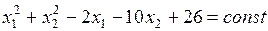определяет окружность, т.к в нём коэффициенты при квадратах координат равны между собой, а член с произведением координат 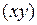отсутствует. Данное уравнение приведём к следующему виду:

.

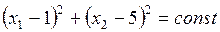Таким образом, центром семейства окружностей будет являться точка .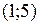

Мини­мальное значение функция 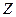прини­мает в точке 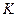, в которой окружность касается области решений.

,

.

,

, ,

.

,

, . .

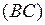
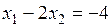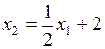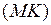
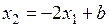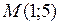
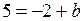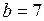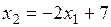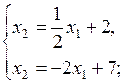
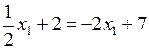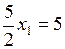
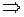
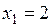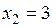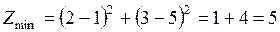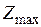достигается в точке . .

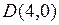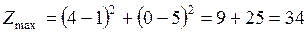Задача 3.

Найти графическим методом минимальное и максимальное значения функции

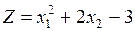при ограничениях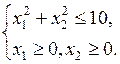

Решение.Линии уровня целевой функции 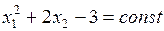. Для разных значений 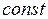графиком уравнения 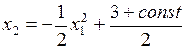является парабола, ветви которой направлены вниз.

1) ;

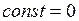
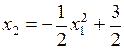
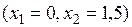2) .

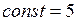
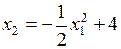
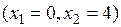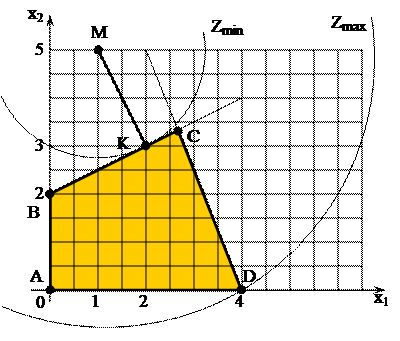
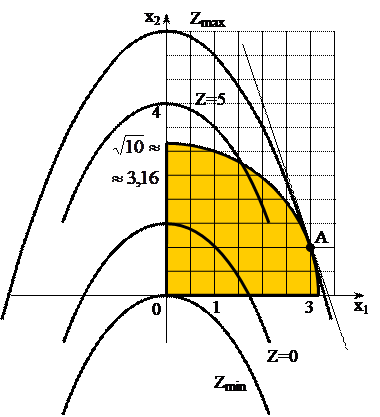
При увеличении 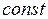параболы сдвигаются вверх, следовательно, минимум целевой функции достигается в начале координат, а максимум – в точке касания соответствующей параболы и окружности .

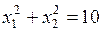Тангенс угла наклона касательной к окружности равен:

.

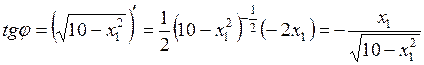Эта же прямая является касательной к параболе .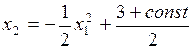

Тангенс угла наклона касательной: .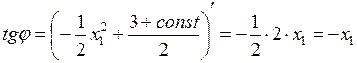

,

,

,

.

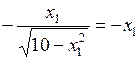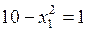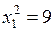
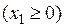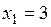Подставляем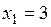

в уравнение окружности:

,

,

.

.

.

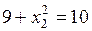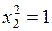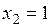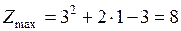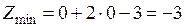Задача 4.

Найти графическим методом минимальное и максимальное значения функции

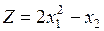при ограничениях