Задание 2.Используя метод множителей Лагранжа, решить следующие задачи.
Задача а) Найти точку условного экстремума функции 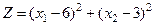
при ограничении 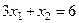 .
.
Решение.
1) Составление функции Лагранжа.
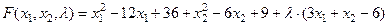 , где
, где 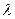 - множитель Лагранжа.
- множитель Лагранжа.
2) Дифференцирование функции 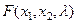 по переменным
по переменным 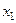 ,
, 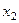 и
и 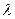 .
.
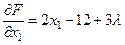 ,
, 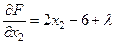 ,
, 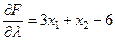 .
.
3)  Составление системы уравнений (для этого полученные выражения частных производных приравнивают к нулю) и решение её.
Составление системы уравнений (для этого полученные выражения частных производных приравнивают к нулю) и решение её.
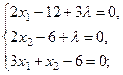
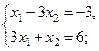
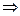
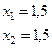
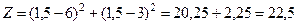 .
.
Задача б) Найти максимальное значение функции 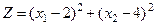
при ограничении 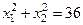 .
.
Решение.
1) Составление функции Лагранжа.
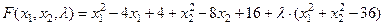 , где
, где 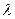 - множитель Лагранжа.
- множитель Лагранжа.
2) Дифференцирование функции 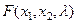 по переменным
по переменным 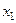 ,
, 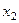 и
и 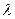 .
.
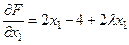 ,
, 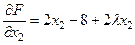 ,
, 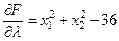 .
.
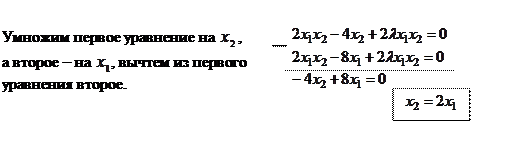 3) Составление системы уравнений (для этого полученные выражения частных производных приравнивают к нулю) и решение её.
3) Составление системы уравнений (для этого полученные выражения частных производных приравнивают к нулю) и решение её.
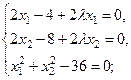
Подставляем в третье уравнение вместо 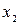 выражение
выражение 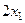 .
.
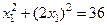 ,
, 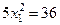 ,
, 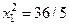 .
.
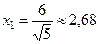 или
или 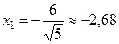 .
.
Тогда 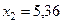 или
или 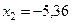 ;
;

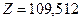 .
.
Ответ. 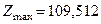 при
при 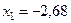 ;
; 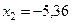 .
.
Практическая работа по теме: