Определение. Задача математического программирования, в которой либо целевая функция, либо ограничения, либо и то, и другое нелинейны, называется нелинейной.
Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведённых товаров – эффект «оптовости».
ЗНП являются очень сложными, поэтому разработаны лишь способы решения отдельных классов ЗНП, и прежде всего задач с выпуклыми (вогнутыми) функциями.
Определение. Множество точек называется выпуклым, если вместе с любыми двумя своими точками оно содержит и весь прямолинейный отрезок, их соединяющий.
На рис. 1множества 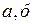 - выпуклые, множества
- выпуклые, множества 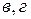 выпуклыми не являются.
выпуклыми не являются.

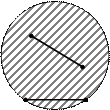
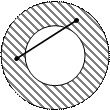
Рис. 1
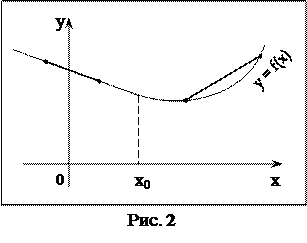 Если функция
Если функция 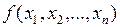 выпуклая на выпуклом множестве
выпуклая на выпуклом множестве  , то геометрически это означает, что отрезок, соединяющий любые две точки её графика, лежит на графике или выше его.
, то геометрически это означает, что отрезок, соединяющий любые две точки её графика, лежит на графике или выше его.
На рис. 2изображён график функ-ции одной переменной, являющейся выпуклой на всей числовой прямой.
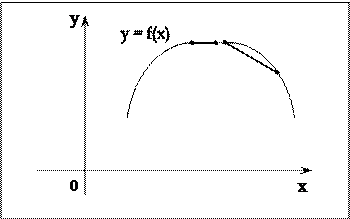 Если отрезок, соединяющий любые две точки графика функции, лежит выше этого графика, то функция является строго выпуклой.
Если отрезок, соединяющий любые две точки графика функции, лежит выше этого графика, то функция является строго выпуклой.
Если функция 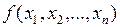 вогнутая на выпуклом множестве
вогнутая на выпуклом множестве  , то геометрически это означает, что отрезок, соединяющий любые две точки её графика, лежит на графике или ниже его (рис. 3).
, то геометрически это означает, что отрезок, соединяющий любые две точки её графика, лежит на графике или ниже его (рис. 3).
Если отрезок, соединяющий любые две точки графика функции, лежит ниже этого графика, то функция является строго вогнутой. Рис. 3
Если 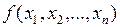 - выпуклая функция, то
- выпуклая функция, то 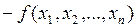 - вогнутая функция, и наоборот.
- вогнутая функция, и наоборот.
Теорема. Пусть 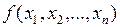 - выпуклая функция, заданная на замкнутом выпуклом множестве
- выпуклая функция, заданная на замкнутом выпуклом множестве 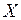 ; тогда любой локальный минимум
; тогда любой локальный минимум 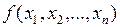 на
на 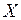 является и глобальным.
является и глобальным.
Следствие 1. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.
Следствие 2. Если 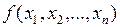 - строго выпуклая функция, то её глобальный минимум на выпуклом множестве
- строго выпуклая функция, то её глобальный минимум на выпуклом множестве  достигается в единственной точке.
достигается в единственной точке.
Теорема. Пусть 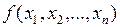 - выпуклая функция, заданная на замкнутом выпуклом множестве
- выпуклая функция, заданная на замкнутом выпуклом множестве  , и, кроме того, она непрерывна вместе со своими частными производными[1] первого порядка во всех внутренних точках
, и, кроме того, она непрерывна вместе со своими частными производными[1] первого порядка во всех внутренних точках 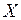 . Пусть
. Пусть 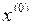 - точка, в которой градиент функции равен нулю. Тогда в точке
- точка, в которой градиент функции равен нулю. Тогда в точке 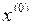 достигается локальный минимум, совпадающий с глобальным минимумом.
достигается локальный минимум, совпадающий с глобальным минимумом.
Градиентом 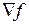 функции
функции 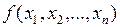 называется вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е.
называется вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е.
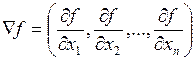 .
.
В каждой точке 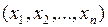 направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.
направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.
Если 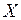 - замкнутое, ограниченное снизу, выпуклое множество, то глобальный максимум выпуклой функции
- замкнутое, ограниченное снизу, выпуклое множество, то глобальный максимум выпуклой функции 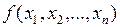 достигается на нём в одной или нескольких крайних точках.
достигается на нём в одной или нескольких крайних точках.
Для вогнутых функций рассмотренные результаты можно сформулировать следующим образом. Пусть 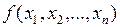 - вогнутая функция, заданная на замкнутом выпуклом множестве
- вогнутая функция, заданная на замкнутом выпуклом множестве 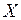 . Тогда любой локальный максимум
. Тогда любой локальный максимум 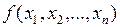 на
на  является глобальным. Если глобальный минимум достигается в двух различных точках множества, то он достигается и в любой точке отрезка, соединяющего данные точки. Для строго вогнутой функции существует единственная точка, в которой она достигает глобального максимума. Глобальный минимум вогнутой функции, если он конечен, на замкнутом, ограниченном снизу множестве, должен достигаться в одной или нескольких его крайних точках.
является глобальным. Если глобальный минимум достигается в двух различных точках множества, то он достигается и в любой точке отрезка, соединяющего данные точки. Для строго вогнутой функции существует единственная точка, в которой она достигает глобального максимума. Глобальный минимум вогнутой функции, если он конечен, на замкнутом, ограниченном снизу множестве, должен достигаться в одной или нескольких его крайних точках.
Если в задачах линейного программирования точки экстремума являются вершинами многогранников решений, то, как следует из рассмотренных ниже примеров, в задачах с нелинейной целевой функцией они могут лежать внутри области, на ребре (грани) или в вершине многогранника.
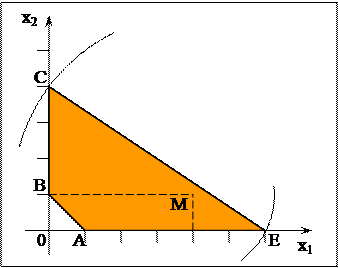
Пример 1. Найти минимальное и максимальное значения функции 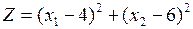 при ограничениях
при ограничениях 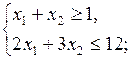
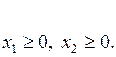
Решение. Область допустимых решений представляет собой многоугольник 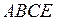 . Если положить
. Если положить 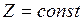
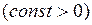 , то получим уравнение окружности
, то получим уравнение окружности
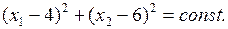
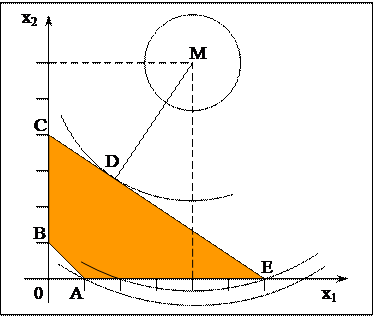 С уменьшением (увеличением)
С уменьшением (увеличением)  (квадрата радиуса) значения функции
(квадрата радиуса) значения функции  соответственно уменьшаются (увеличиваются).
соответственно уменьшаются (увеличиваются).
Проводя из точки  окружности различных радиусов, получаем: минимальное значение функция
окружности различных радиусов, получаем: минимальное значение функция 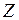 принимает в точке
принимает в точке 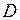 , в которой окружность касается области решений.
, в которой окружность касается области решений.
Точка 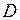 не является угловой, её координаты находят в результате решения системы уравнений, соответствующих прямым
не является угловой, её координаты находят в результате решения системы уравнений, соответствующих прямым 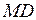 и
и 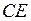 .
.
Для двух перпендикулярных прямых
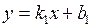 и
и 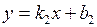 выполняется соотношение:
выполняется соотношение:
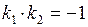 (или
(или 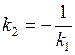 ). Уравнение прямой
). Уравнение прямой  :
: 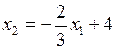 .
.
Тогда уравнение прямой 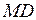 :
: 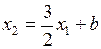 .
.
Для определения 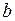 воспользуемся тем, что эта прямая проходит через точку
воспользуемся тем, что эта прямая проходит через точку 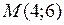 :
:
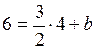 ,
, 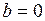 . Т.е. уравнение прямой
. Т.е. уравнение прямой 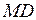 :
: 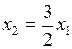 .
.
Определяем координаты точки 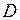 :
:

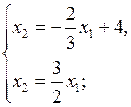
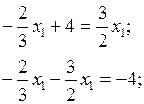
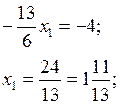
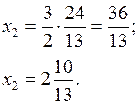
Минимальное значение функции:
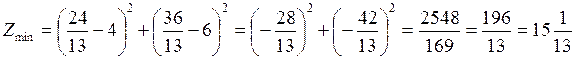 .
.
Функция 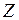 имеет два локальных максимума:
имеет два локальных максимума:
в вершине 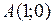 функция
функция 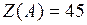 , в вершине
, в вершине 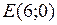 функция
функция 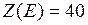 .
.
Так как 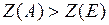 , то вершина
, то вершина 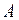 - точка глобального максимума.
- точка глобального максимума.
Ответ: 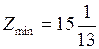 при
при 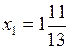 ,
, 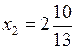 ;
; 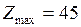 при
при 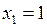 ,
, 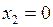 .
.
Пример 2. Пусть область допустимых решений останется прежней, а
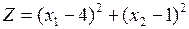 .
.
Найти минимальное и максимальное значения этой функции.
 Решение.
Решение.
Минимальное значение функция принимает в точке 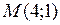 :
: 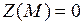 . Функция
. Функция 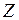 имеет два локальных максимума:
имеет два локальных максимума:
в вершине 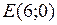 функция
функция 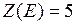 ,
,
в вершине 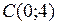 функция
функция 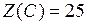 , т.е. глобальный максимум достигается в вершине
, т.е. глобальный максимум достигается в вершине 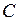 .
.
Ответ: 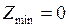 при
при 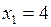 ,
, 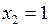 ;
;
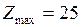 при
при 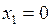 ,
, 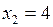 .
.
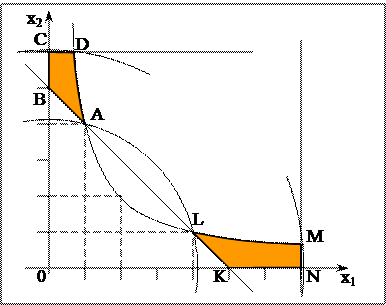
Пример 3. Найти минимальное и максимальное значение функции
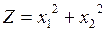
при ограничениях 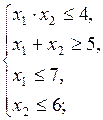
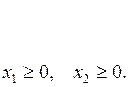
 Решение.
Решение.
В этом случае область допустимых решений не является выпуклой и состоит из двух отдельных частей.
Минимальное значение функции 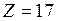 достигается в точках
достигается в точках 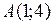 и
и 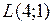 .
.
Функция 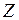 имеет два локальных максимума:
имеет два локальных максимума:
в точке 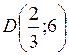 функция
функция 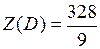 и в точке
и в точке 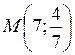 функция
функция 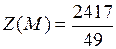 . Точка
. Точка 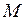 является точкой глобального максимума.
является точкой глобального максимума.

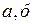 - выпуклые, множества
- выпуклые, множества  выпуклыми не являются.
выпуклыми не являются.



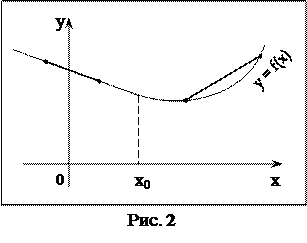 Если функция
Если функция 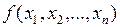 выпуклая на выпуклом множестве
выпуклая на выпуклом множестве 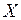 , то геометрически это означает, что отрезок, соединяющий любые две точки её графика, лежит на графике или выше его.
, то геометрически это означает, что отрезок, соединяющий любые две точки её графика, лежит на графике или выше его.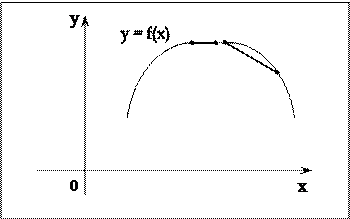 Если отрезок, соединяющий любые две точки графика функции, лежит выше этого графика, то функция является строго выпуклой.
Если отрезок, соединяющий любые две точки графика функции, лежит выше этого графика, то функция является строго выпуклой.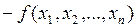 - вогнутая функция, и наоборот.
- вогнутая функция, и наоборот.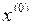 - точка, в которой градиент функции равен нулю. Тогда в точке
- точка, в которой градиент функции равен нулю. Тогда в точке 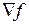 функции
функции 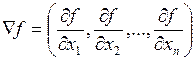 .
.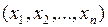 направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.
направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.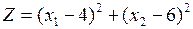 при ограничениях
при ограничениях 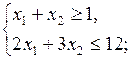
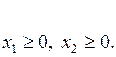
 . Если положить
. Если положить 
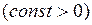 , то получим уравнение окружности
, то получим уравнение окружности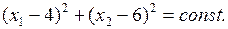
 С уменьшением (увеличением)
С уменьшением (увеличением) 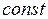 (квадрата радиуса) значения функции
(квадрата радиуса) значения функции  соответственно уменьшаются (увеличиваются).
соответственно уменьшаются (увеличиваются).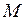 окружности различных радиусов, получаем: минимальное значение функция
окружности различных радиусов, получаем: минимальное значение функция 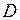 , в которой окружность касается области решений.
, в которой окружность касается области решений.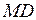 и
и 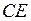 .
.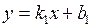 и
и 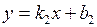 выполняется соотношение:
выполняется соотношение: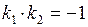 (или
(или 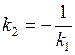 ). Уравнение прямой
). Уравнение прямой 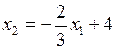 .
.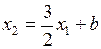 .
. воспользуемся тем, что эта прямая проходит через точку
воспользуемся тем, что эта прямая проходит через точку 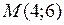 :
: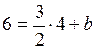 ,
, 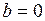 . Т.е. уравнение прямой
. Т.е. уравнение прямой 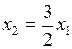 .
.
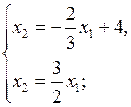
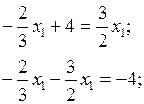
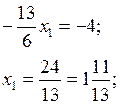
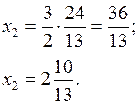
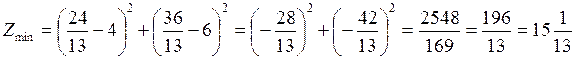 .
.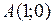 функция
функция 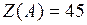 , в вершине
, в вершине 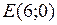 функция
функция 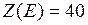 .
.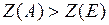 , то вершина
, то вершина 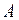 - точка глобального максимума.
- точка глобального максимума.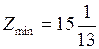 при
при 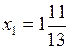 ,
, 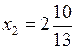 ;
; 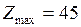 при
при 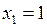 ,
, 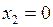 .
.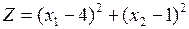 .
. Решение.
Решение.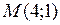 :
: 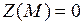 . Функция
. Функция 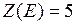 ,
,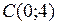 функция
функция 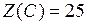 , т.е. глобальный максимум достигается в вершине
, т.е. глобальный максимум достигается в вершине 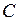 .
.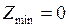 при
при 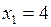 ,
, 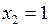 ;
;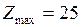 при
при 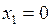 ,
, 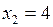 .
.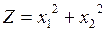
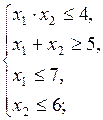
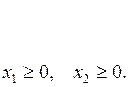
 Решение.
Решение.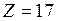 достигается в точках
достигается в точках 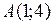 и
и 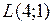 .
.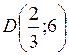 функция
функция 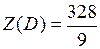 и в точке
и в точке 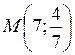 функция
функция 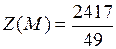 . Точка
. Точка