а) Пусть на отрезке [a,b] задана непрерывная функция f(х)³0(рис. 4а).
Если криволинейная трапеция, ограниченная кривой у=f(х) и прямыми у=0, х=а и х=b, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле: 
. (1)
а) б)
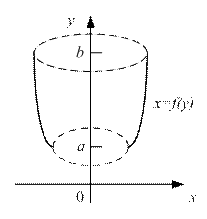
Рисунок 4
Пример. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривой 
и 0£х£2.
(куб.ед.).
б) Пусть на отрезке [a,b] оси Оу задана непрерывная функция f(у)³0(рис. 4а). Тогда объем полученного при вращении вокруг оси Оу тела вычисляется по формуле: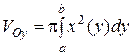 
. (2)
Пример. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривой при 1£у£4.
(куб. ед.).
в) Пусть на отрезке [a,b] заданы непрерывные функции f1(х)³0 и f2(х)³0(f1(х)£f2(х)). Тогда, если фигура, ограниченная линиями у=f1(х), у=f2(х) и прямыми х=а и х=b, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле: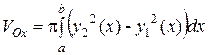 
. (3)
Пример. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 
и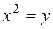 
(рис. 5).
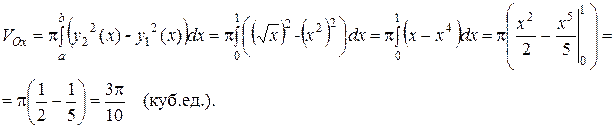
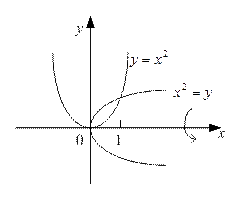
Рисунок 5
