Использование этих законов позволяет упрощать исходную запись ФАЛ.

Вернемся к анализу ФАЛ, представленной в таблице 3.

В первой исходной записи ФАЛ, полученной по таблице 3, в каждом логиче­ском произведении переменных (конъюнкция) присутствовали все переменные из набора x₁x₂x₃, а сами конъюнкции соединены символом логического сложения (дизъюнкции). Такая форма записи ФАЛ называется совершенной дизъюнктивной нормаль­ной формой (СДНФ).

Если не все переменные из набора x₁x₂x₃ представлены в каждой из конъ­юнкций, то такая форма по прежнему остается нормальной дизъюнктивной фор­мой, но она не относится к классу совершенных.

ДНФ представления одной и той же ФАЛ может быть много, но совершенная ДНФ (СДНФ) одна единственная.

Кроме СДНФ существует так называемая конъюнктивная нормальная форма, которая также может быть совершенной (СКНФ) и не совершенной, т.е. просто КНФ.

КНФ представляет собой алгебраическое выражение в виде стольких конъюнктивных членов, представляющих со­бой дизъюнкции всех переменных, при скольких наборах значений переменных функция равна 0. Если в наборе значение переменной равно 1, в дизъюнкцию входит инверсия этой переменной.

Анализ СДНФ и СКНФ показывает неэкономичность записи ФАЛ. Исполь­зуя свойства ФАЛ можно преобразовать выражения за счет так называемой операции склеивания, т.е.

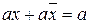, т.к. .

,

где a – любая ФАЛ.

Упрощение записи СДНФ за счет операции склеивания называется миними­зацией ФАЛ.