Операции алгебры логики обладают свойствами, аналогичными операциям сложения и умножения обычной алгебры.
На основании этих законов можно выносить переменные за скобки, переставлять местами и т.д., как и в обычной алгебре.
Мы говорили о законе склеивания, поглощения, распределительный закон, сочетательный закон, переместительный закон,
Но только для алгебры логики действует закон двойственности (правило де Моргана):
; 
= 
.
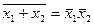Законы двойственности обобщены К. Шенноном для любых булевых функций (ФАЛ):
.
Такая запись обозначает тот факт, что отрицание над записью всей функции приводит к отрицанию значения переменных и знаков, их соединяющих, т.е. дизъюнкция ( 
) заменяется знаком конъюнкции ( 
), и наоборот.
Пример:
(*)
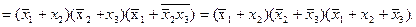Заметим, что в первоначальную запись функции (*) можно значительно упростить. Действительно, вынесем за скобки 
, тогда получим:
