Функция f(x1,…,xn) называется линейной, если ее можно представить в виде полинома Жегалкина не выше первой степени, т.е. если существуют такие константы Ai, i=1,…,n, что 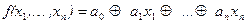 .
.
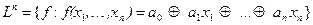
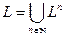
Пример 12. Функции 0,1, x, Øx, xÅy, x~y Î L, а x&y, xÚy Ï L.
Лемма 6.|Ln|= 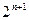 .
.
Лемма 7.[L]= L.
Лемма 8.Функция является линейной тогда и только тогда, когда она меняет свое значение на любой паре соседних по существенной переменной наборов.
Лемма 9.(лемма о нелинейной функции) Если fÏL, то x&yÎ[{f,0,1,Øx}].