Полиномом Жегалкина называется бесскобочная форма записи формулы в алгебре Жегалкина.
Любая булева функция может быть представлена полиномом Жегалкина, поскольку любая ДНФ или КНФ с помощью равенств (3.1.) и (3.2.) может быть преобразована в формулу алгебры Жегалкина, в которой всегда можно избавиться от скобок (если они там есть) с помощью тождества 5 (дистрибутивность 
относительно 
) [4].
Пример3.1. Найти полином Жегалкина для булевой функции эквиваленция.
Решение. С учетом (3.1.) и (3.2.) имеем
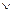
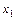
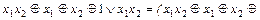
Получили полином Жегалкина для эквиваленции
. (3.3.)
Булева функция называется линейной, если ее полином Жегалкина не содержит операции конъюнкции. В противном случае булева функция называется нелинейной.
Линейные функции это сама операция сложения по модулю два 
, а также инверсия и эквиваленция (соотношения (3.1.) и (3.3.) соответственно). Примерами нелинейных булевых функций являются конъюнкция (ее полином Жегалкина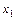 
), дизъюнкция, т.к., согласно (3.2.), ее полином содержит конъюнкцию и ряд других функций.
Совокупность всех линейных булевых функций далее будем обозначать классом 
.
Пример 3.2. Проверить свойство линейности для импликации.
Решение. Вычислим полином Жегалкина для импликации, используя соотношения.
Получим
.
Импликация – нелинейная функция, поскольку ее полином Жегалкина содержит конъюнкцию двух переменных
. (2.4.)
