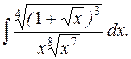Интегралы типа  называются интегралами от дифференциального бинома, где a,b – действительные числа; m, n, и p – рациональные числа.
называются интегралами от дифференциального бинома, где a,b – действительные числа; m, n, и p – рациональные числа.
Как было доказано Чебышевым П.А., интеграл от дифференциального бинома может быть выражен через элементарные функции только в следующих трех случаях:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки  , где l - общий знаменатель m и n.
, где l - общий знаменатель m и n.
2) Если  - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой
 , где s – знаменатель числа р.
, где s – знаменатель числа р.
3) Если  - целое число, то используется подстановка
- целое число, то используется подстановка  , где s – знаменатель числа р.
, где s – знаменатель числа р.
Во всех остальных случаях интегралы типа  не выражаются через известные элементарные функции.
не выражаются через известные элементарные функции.
Пример. Найти интеграл I =  .
.
Так как дифференциальный бином -  ,
,
то  . Поэтому делаем подстановку
. Поэтому делаем подстановку  ,
,
тогда  ,
,  . В результате
. В результате
I =  =
= 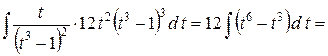
=  .
.
Примеры для самостоятельного решения
Найти интеграл
1)  . 2)
. 2)  . 3)
. 3)  . 4)
. 4)  . 5)
. 5)  .
.
6)  . 7)
. 7)  . 8)
. 8)  . 9)
. 9)  . 10)
. 10)  .
.
11)  . 12)
. 12)  . 13)
. 13)  . 14)
. 14)  .
.
15) 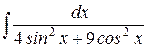 . 15)
. 15) 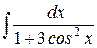 . 16)
. 16) 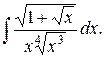 17)
17) 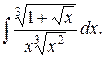
18)  19)
19)  20)
20)