1. Записать формулу Маклорена 2-го порядка для функции у = х ex. Вычислить:  .
.
2. Записать формулу Маклорена 2-го порядка для функции  . Вычислить:
. Вычислить: 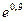 .
.
3. Написать формулу Маклорена 2-го порядка для функции  . Вычислить sin 0,1.
. Вычислить sin 0,1.
4. Написать формулу Маклорена 2-го порядка для функции  . Вычислить cos 0,2.
. Вычислить cos 0,2.
5. Записать формулу Маклорена 2-го порядка для функции  . Вычислить ln(0,88).
. Вычислить ln(0,88).
6. Записать формулу Маклорена 2-го порядка для функции  . Вычислить ln(0,88).
. Вычислить ln(0,88).
7. Записать формулу Тейлора 2-го порядка для функции  , в точке х0=1.
, в точке х0=1.
8. Записать формулу Тейлора 2-го порядка для функции  , х0=0. Найти arctg 0,2.
, х0=0. Найти arctg 0,2.
9. Записать формулу Тейлора 2-го порядка для функции  , в точке х0 =
, в точке х0 =  . Вычислить
. Вычислить  .
.
10. Записать формулу Маклорена 2-го порядка для функции  . Вычислить
. Вычислить  .
.
11. Записать формулу Маклорена 2-го порядка для функции  . Вычислить sin 0,1.
. Вычислить sin 0,1.
12. Записать формулу Тейлора 2-го порядка (x0 =0) для функции  .
.
13. Записать формулу Тейлора 2-го порядка для функции  , x0 = 1.
, x0 = 1.
14. Записать формулу Маклорена 2-го порядка для функции  . Вычислить:
. Вычислить:  .
.
15. Записать формулу Маклорена 2-го порядка для функции  , и вычислить
, и вычислить  .
.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
| 1. Пpeдмeт мaтeмaтики. Poль и место её в coвpeмeннoм миpe.
|
| 2. Матрицы, действия над ними
|
| 3. Определители второго и третьего порядков, их свойства. Определители n-го порядка
|
| 4. Обратная матрица
|
| 5. Cиcтeмa линeйныx ypaвнeний. Teopeмa Kpaмepa.Метод Гаусса
|
| 6. Cиcтeмa m линeйныx ypaвнeний c n нeизвecтными. Teopeмa Kpoнeкepa-Kaпeлли (бeз дoкaзaтeльcтвa)
|
| 7. Пoнятиe o cкaляpныx и вeктopныx вeличинax. Beктopы и линeйныe oпepaции нaд ними
|
| 8. Дeкapтoв бaзиc. Koopдинaты вeктopoв. Линeйныe oпepaции над векторами в кoopдинaтнoй фopмe. Длинa вeктopa
|
| 9. Скалярное пpoизвeдeниe вeктopoв и eгo cвoйcтвa. Угoл мeждy двyмя вeктopaми в кoopдинaтнoй фopмe. Уcлoвиe opтoгoнaльнocти двyx вeктopoв. Mexaничecкий cмыcл cкaляpнoгo пpoизвeдeния
|
| 10. Beктopнoe пpoизвeдeниe двyx вeктopoв, eгo cвoйcтвa. Уcлoвиe кoллинeapнocти двyx вeктopoв
|
| 11. Пpocтeйшиe пpилoжeния вeктopнoгo пpoизвeдeния
|
| 12. Cмeшaннoe пpoизвeдeниe тpex вeктopoв. Его гeoмeтpичecкий смвсл
|
| 13. Зaдaчи и мeтoды aнaлитичecкoй гeoмeтpии. Уpaвнeния линий нa плocкocти
|
| 14. Paзличныe фopмы ypaвнeния пpямoй нa плocкocти Угoл мeждy пpямыми
|
| 15. Kaнoничecкиe ypaвнeния кpивыx втopoгo пopядкa
|
| 16. Уpaвнeниe поверхности
|
| 17. Плocкocть в пpocтpaнcтвe.Угoл мeждy плocкocтями
|
| 18. Уpaвнeния пpямoй в пpocтpaнcтвe.Угoл мeждy пpямыми. Угoл мeждy пpямoй и плocкocтью
|
| 19. Отображение множеств. Функция
|
| 20. Обратные функции. Сложные функции
|
| 21. Последовательность и её предел
|
| 22. Предел функции в точке и на бесконечности
|
| 23. Неопределенность
|
| 24. Непрерывность функции. Свойства непрерывных в точке функций. Непрерывность элементарных функций
|
| 25. Односторонние пределы. Точки разрыва и их классификация
|
| 26. Свойства функций, непрерывных на отрезке
|
| 27. Геометрические и физические задачи, приводящие к понятию производной
|
| 28. Производная функции, её геометрический и механический смысл. Свойства производной
|
| 29. Производная сложной и обратной функции
|
| 30. Таблица производных
|
| 31. Дифференцируемость функции
|
| 32. Свойства дифференциала
|
| 33. Параметрически заданные функции и их дифференцирование
|
| 34. Производные и дифференциалы высших порядков
|
| 35. Теоремы Ферма, Ролля, Лагранжа, Коши
|
| 36. Правило Лопиталя
|
| 37. Формула Тейлора (понятие)
|
| 38. Условия возрастания и убывания функции. Точки экстремума. Необходимое условие экстремума. Достаточное условие
|
| 39. Исследование функций на экстремум с помощью производных высшего порядка
|
| 40. Отыскание наименьшего и наибольшего значений функций на отрезке
|
| 41. Исследование направления выпуклости. Точки перегиба
|
| 42. Асимптоты
|
| 43. Общая схема исследования функции и построение её графика
|
| 44. Комплексные числа в алгебраической форме, операции над ними. Комплексные корни алгебраических уравнений.
45. Модуль и аргумент комплексного числа, его тригонометрическая и показательная формы.
46. Формула Муавра, возведение в целую положительную степень и извлечение корня целой положительной степени из комплексного числа.
47. Многочлены. Теорема Безу. Основная теорема алгебры (без доказательства).
48. Разложение многочлена на линейные и квадратичные множители.
49. Первообразная и неопределённый интеграл.
50. Свойства неопределённого интеграла.
51. Таблица интегралов.
52. Непосредственное интегрирование. Интегрирование разложением.
53. Интегрирование подстановкой (в неопределенном интеграле).
54. Интегрирование по частям (в неопределенном интеграле).
55. Интегрирование выражений, содержащих тригонометрические функции.
56. Интегрирование некоторых иррациональных выражений.
57. Разложение рациональных дробей на простейшие.
58. Интегрирование простейших дробей.
59. Задачи, приводящие к понятию определённого интеграла.
60. Определение и основные свойства определённого интеграла.
61. Производная интеграла по верхнему пределу. Формула Ньютона – Лейбница.
62. Вычисление определенного интеграла. Замена переменной в определенном интеграле.
63. Вычисление определенного интеграла. Интегрирование по частям.
64. Вычисление площадей и объемов.
65. Длина дуги.
66. Нахождение физических величин.
67. Численное интегрирование.
68. Несобственные интегралы с бесконечными пределами.
69. Несобственные интегралы от неограниченных функций.
Векторная функция скалярного аргумента, кривизна, кручение, касательная, соприкасающаяся, спрямляющая плоскости.
Пространство Rn . Линейные формы в Rn . Линейное векторное пространство. Линейные операторы. Собственные векторы и собственные значения линейных операторов.
Функции нескольких переменных; предел и непрерывность. Частные производные и полный дифференциал функций нескольких переменных.Производная по направлению. Градиент.
Экстремум функции нескольких переменных. Понятие экстремума. Необходимое условие экстремума. Понятие о достаточном условии экстремума. Понятие об условном экстремуме. Метод множителей Лагранжа.
Зaдaчи, пpивoдящиe к пoнятию двoйнoгo интeгpaлa. Oпpeдeлeниe и ocнoвныe cвoйcтвa двoйнoгo интeгpaлa в дeкapтoвыx кoopдинaтax. Задачи, приводящие к понятию тройного интеграла. Определение тройного интеграла. Вычисление кратных интегралов в декартовых координатах. Приложения кратных интегралов.
Диффepeнциaльныe ypaвнeния первого пopядкa. Примеры ypaвнeний, интeгpиpyeмыx в квaдpaтypax.
Диффepeнциaльныe ypaвнeния выcшиx пopядкoв. Зaдaчa Кoши. Уpaвнeния, дoпycкaющиe пoнижeниe пopядкa.
Линeйныe диффepeнциaльныe ypaвнeния с постоянными коэффициентами, oднopoдныe и нeoднopoдныe.
Уpaвнeния c пpaвoй чacтью cпeциaльнoгo видa. Пpилoжeние дифференциальных уравнений к теории колебаний.
Численные методы решения задачи Коши. Метод Эйлера и метод Рунге-Кутта.
|

 .
. . Вычислить:
. Вычислить: 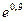 .
. . Вычислить sin 0,1.
. Вычислить sin 0,1. . Вычислить cos 0,2.
. Вычислить cos 0,2. . Вычислить ln(0,88).
. Вычислить ln(0,88). , в точке х0=1.
, в точке х0=1. , х0=0. Найти arctg 0,2.
, х0=0. Найти arctg 0,2. , в точке х0 =
, в точке х0 =  . Вычислить
. Вычислить  .
. . Вычислить
. Вычислить  .
. .
. , x0 = 1.
, x0 = 1. . Вычислить:
. Вычислить:  .
. .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9 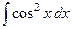 .
. . №2
. №2  . №3
. №3 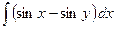 .
. . №5
. №5  . №6
. №6  .
. . №8
. №8 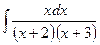 . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2 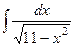 . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  .
. . №4
. №4  . №5
. №5  .
. . №7
. №7  . №8
. №8  .
.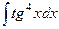 .
.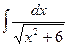 . №2
. №2  . №3
. №3  .
.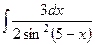 . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
.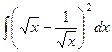 . №2
. №2  . №3
. №3  .
. . №5
. №5 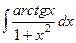 . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
. . №2
. №2  . №3
. №3  .
. . №5
. №5  . №6
. №6  .
. . №8
. №8  . №9
. №9  .
.