Теорема. Производная интеграла по переменной верхней границе равна подынтегральной функции, в которой переменная интегрирования заменена верхней границей.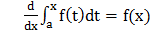 
Доказательство. Для нахождения производной функции 
дадим x приращение ∆x.
Тогда новое значение функции равно I(x+∆x)=
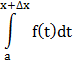
Тогда приращение функции при переходе от точки x к точке x+∆x окажется равным
∆I=I(x+∆x)-I(x)=
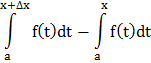
Тогда по третьему свойству
, то есть ∆I=
(2)
Применим к интегралу (2) теорему о среднем 
где 
заключено между x и x+∆x. Итак, 
Пользуясь теперь определением производной, получим 
.
Но, учитывая, что при ∆x→0 x+∆x→x, то есть и →x. Причем, подынтегральная функция непрерывна в точке x. Поэтому, 
= 
.
Итак, 
, что и требовалось доказать.
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
