Рассматривая частные производные 
и 
как функции от 
, приходим к понятиям частных производных второго порядка. А именно, выражения
, 
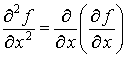
называют частными производными второго порядка функции 
по x и y по соответственно, а выражения
, 
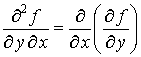
– смешанными частными производными второго порядка функции . Их обозначают также символами: 
, 
, 
и 
. Аналогично определяют частные производные 3-го порядка (их будет 8=23 ), 4-го порядка (их будет 16=24 ) и т.д.
Теорема 4. Если в некоторой окрестности точки 
функция 
имеет смешанные частные производные 
и 
, причем эти производные непрерывны в точке 
, то они равны в этой точке:
= 
.
Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции не зависят от порядка дифференцирования в точке .
Теорема 4 допускает обобщение: по индукции ее можно распространить на любые непрерывные смешанные частные производные.
3. 
4. 
