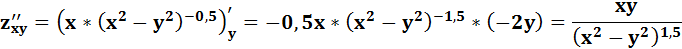Дифференциал функции двух переменных.

Пусть функция z = f(x,y), имеет в точке М₀(х₀,у₀) частные производные f ^/_x (х₀,у₀) и f ^/_у (х₀,у₀).

О. Полным приращением функции z = f(x,y) в точке М₀(х₀,у₀) называется разность 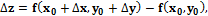где ∆x и ∆y-произвольные приращения аргументов.

Пусть приращение функции z =f(x,y) можно представить в виде где , то функция называется дифференцируемой в точке M ₀ (х₀,у₀).

О. Полным дифференциалом функции z=f(x,y) называется главная часть полного приращения ∆z , линейная относительно приращений её аргументов ∆x и ∆y . Полный дифференциал функции (если он существует) равен сумме всех ее частных дифференциалов и вычисляется по формуле: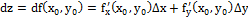

При достаточно малых (по абсолютному значению) приращениях аргументов, полное приращение функции можно с как угодно малой относительной погрешностью заменить ее полным дифференциалом. Дифференциалы dх и dy независимых аргументов функции х и у совпадают с их приращениями соответственно ∆x и ∆y . Таким образом,

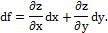
3.

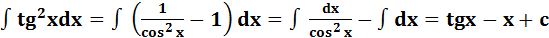
4.