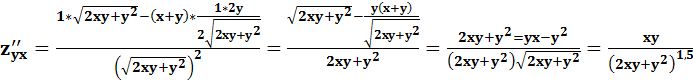Интегрирование тригонометрических функций.Уневерсальная тригонометрическая подстановка.
Инвариантность формы первого дифференциала функции двух переменных.
Итак,если x является независимой переменной,то дифференциал функции 
можно записать так: 
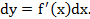
Покажем,что эта форма сохраняется и в случае,если x является не независимой переменной, а функцией.Действительно ,пусть и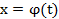 
,то есть y –сложная функция от 
. Тогда,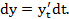 
По правилу дифференцирования сложной функции: 
. 
Этим мы доказали следующее:
Теорема.Дифференциал сложной функции ,для которой 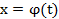,имеет такой же вид, 
,как и в том случае,когда аргумент x является независимой переменной.Это свойство называется- инвариантность формы дифференциала.
3. 
4. 
