После введения трех операций над предикатами возникают вопросы: как они влияют на равносильность предикатов и каковы закономерности образования с помощью этих операций равносильных предикатов? Аналогичны вопросы для следования предикатов. Ответ дает следующая теорема.
Теорема 19.12. Если во всех формулах теоремы 3.2 под 
понимать предикаты, определенные на соответствующих множествах, знак 
всюду заменить знаком 
, а знак 
— знаком 
, то получим верные утверждения о предикатах.
Доказательство. Рассмотрим, например, вторую из формул д) теоремы 3.2. Она превращается в следующее утверждение:
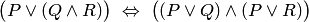
означающее равносильность предикатов 
и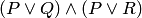 
независимо от предикатов . Проверим, верно ли данное утверждение. В самом деле, каждый из двух предикатов при любой подстановке вместо предметных переменных конкретных предметов из соответствующих множеств превращается в такое высказывание, которое на основании тавтологии из теоремы 3.2 (пункт д) имеет одинаковые значения истинности. На основании определения равносильности предикатов это и означает, что данные предикаты равносильны.
