|
Аксиомы
(тождества)
Переместительный закон
|  (10.6) (10.6)
|
 (10.7) (10.7)
|
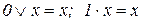 (10.8) (10.8)
|
 (10.9) (10.9)
|
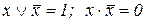 (10.10) (10.10)
|
 (10.11) (10.11)
|
 (10.12) (10.12)

|
| Сочетательный закон
|  (10.13) (10.13)
|
| Распределительный закон
|  (10.14) (10.14)
|
| Закон инверсии
(закон Де Моргана)
|  (10.15) (10.15)
|
| Закон поглощения
| 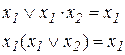 (10.16) (10.16)
|
| Закон склеивания
| 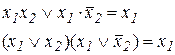 (10.17) (10.17)
|
Как отмечалось выше, для преобразования алгебраических выражений используют тождества (аксиомы) и законы булевой алгебры. Основные из них приведены в таблице 10.6.
В ней алгебраические выражения тождеств и законов заданы парами на основании принципа дуальности (двойственности), согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять логическую 1 на 0, 0 на 1, знак \/ на ∙ , а ∙ на \/ .
Применение аксиом и законов булевой алгебры покажем на примере преобразования функции у10 из СКНФ в СДНФ. Для этого можно использовать распределительный закон (10.14), затем тождество (10.10):
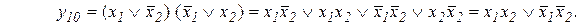
Перейдем к четвертому вопросу лекции.