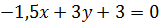Прямая линия и её уравнения

Общее уравнение прямой: Аx+Вy+С=0

Векторное уравнение прямой: А(x-x₀)+В(y-y₀)+С=0

Каноническое уравнение прямой: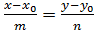

Уравнение прямой в отрезках: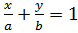

Уравнение прямой с угловым коэффициентом: y=kx+b, k=tgα=y₀/x₀

y-y₀=k(x-x₀)

Уравнение прямой проходящей через две точки: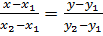

Угол между двумя прямыми: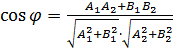

Условие параллельности двух прямых: , ,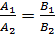

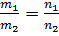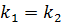
Условие перпендикулярности двух прямых: , ,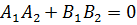

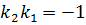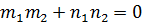
Расстояние d от точки М₀ (x₀;y₀) до прямой Аx+Вy+С=0: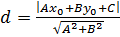

Пример 2: Даны вершины треугольника A(3;4), B(6;2), C(3;1/2). Составить: 1) уравнение стороны AB; 2) длину высоты треугольника, проведенной из вершины C; 3) уравнение прямой, проходящей через вершину C параллельно прямой AB; 4) внутренний угол B.

Решение: Сделаем чертеж (Рис. 2)

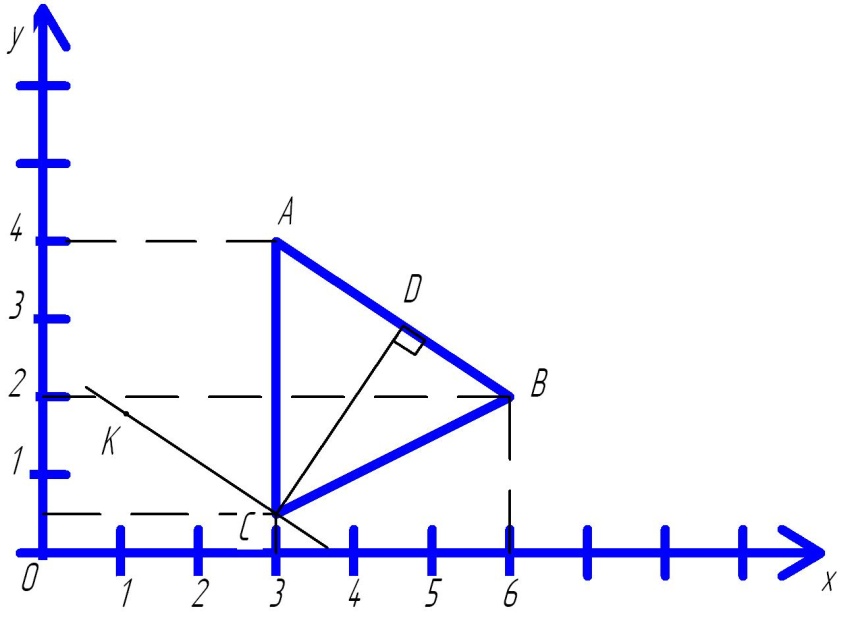
Рисунок 2 – Чертеж задачи

1) По формуле: 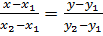; AB: 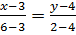=> -2(x-3)=3(y-4) => -2x+6=3y-12 => -2x-3y+18=0

2) Проведем высоту CD. Длина отрезка CD – расстояние от точки C до прямой AB, так как CD ┴ AB => по формуле 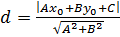, где ( 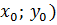- координаты точки C, а коэффициенты A, B, C – из уравнения прямой AB.

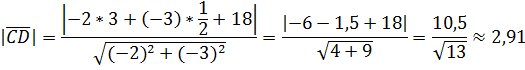
3) Проведем прямую KC ║ AB. Из уравнения AB выразим y и найдем K₁.

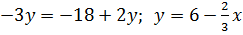=> K₁= 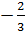. Так как KC ║ AB =>

K₂ = K₁ = 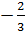и KC проходит через точку C (3;1/2) =>

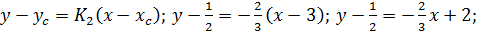
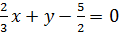- это уравнение KC

4) Внутренний угол B – это угол между прямыми AB и BC.

По формуле: ;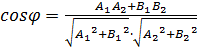

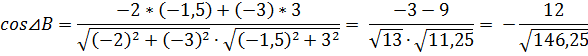
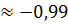
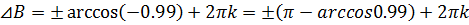
Так как BC: => => =>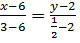

;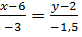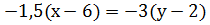
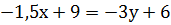