При выяснении геометрического смысла определенного интеграла, мы получили формулу для нахождения площади криволинейной трапеции, ограниченной осью Ох, прямыми x = a, x = b и непрерывной неотрицательной (неположительной) функцией y = f(x). В некоторых случаях функцию, которая ограничивает фигуру, удобно задать в параметрическом виде, то есть, представить функциональную зависимость через параметр t. В этой статье мы разберемся, как находить площадь фигуры в случае параметрического задания ограничивающей кривой.
После краткого обзора теории и вывода формулы, мы подробно рассмотрим решение характерных примеров на нахождение площади.
Пусть границами криволинейной трапеции являются прямые x = a, x = b, ось абсцисс и параметрически заданная кривая  , причем функции
, причем функции  и
и  непрерывны на интервале
непрерывны на интервале  ,
,  монотонно возрастает на нем и
монотонно возрастает на нем и  .
.
Тогда площадь криволинейной трапеции находится по формуле  .
.
Эта формула получается из формулы площади криволинейной трапеции  подстановкой
подстановкой  :
:
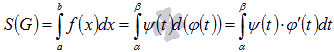
Если функция  является монотонно убывающей на интервале
является монотонно убывающей на интервале  , то формула примет вид
, то формула примет вид  .
.
Если функция  не является основной элементарной, то для выяснения ее возрастания или убывания может потребоваться теория из раздела возрастание и убывание функции на интервале.
не является основной элементарной, то для выяснения ее возрастания или убывания может потребоваться теория из раздела возрастание и убывание функции на интервале.