Для характеристики среднего значения СВ вводится математическое ожидание.
О: Математическим ожиданием дискретной СВ 
с законом распределения 
называется
. (14.2)
О: Математическим ожиданием непрерывной СВ 
с плотностью распределения 
называется
(14.3)
Если задана дискретная СВ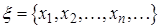 
с законом распределения 
, то математическое ожидание определяется как 
в случае абсолютной сходимости ряда справа. В противном случае СВ не имеет математического ожидания.
Для характеристики степени разбросанности значений СВ около её среднего значения вводится дисперсия.
О: Дисперсией СВ называется
. (14.4)
О: Средним квадратичным отклонением СВ называется
. (14.5)
Дисперсию вычисляют по формуле
.
Примеры.
1) Бросается игральная кость.
.
.
.
