Нехай P(x, y) та Q(x, y) – функції двох змінних, які є безперервні в деякій області D і L – гладка лінія, яка цілком розміщена у цій області. Розіб’ємо лінію L на n частин в напрямі від А до В (Рис. 25). У кожній такій частині виберемо довільну точку Мі (xі, hі), позначимо проекції вектора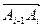 
на осі координат через 
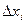та 
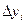і складемо дві суми:
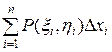та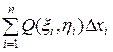 
, (5.1)
де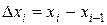 
– проекція дуги 
на вісь ОХ, – на вісь ОУ.
Сума (5.1) називається інтегральною сумою для функції P(x, y) і Q(x, y) за змінною х та у відповідно вздовж кривої АВ.
Означення. Якщо інтегральна сума (5.1) при l 
0 має скінченну границю, яка не залежить ні від розбиття кривої АВ, ні від вибору точок Мі, то цю границю називають криволінійним інтегралом від функцій P(x, y) та Q(x, y) за координатами х та у вздовж кривої АВ і позначають:
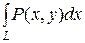та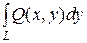 
.
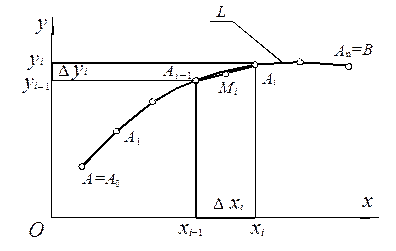
Рис. 25
Таким чином,
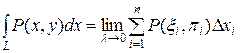, та
.
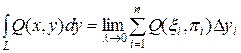Суму +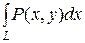 
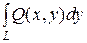називають криволінійним інтегралом за координатами або криволінійним інтегралом другого роду від функцій P(x, y) та Q(x, y) по кривій АВ і позначають символом:
.
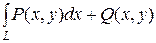Остаточно, криволінійним інтегралом за координатами від виразу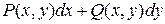 
по направленій дузі L називається границя інтегральних сум, коли 
:
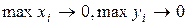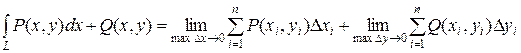. (5.2)
Механічний зміст: якщо змінна сила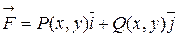 
виконує роботу А при переміщенні матеріальної точки вздовж кривої АВ, причому функції P(x, y) та Q(x, y), неперервні на кривій, то здійснена робота обчислюється за формулою:
.
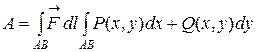