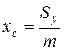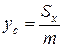,
.
6. Моменти інерції.Для кривої АВ моменти інерції щодо осей ОХ, ОУ та початку координат відповідно рівні:
,
,
.
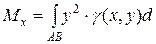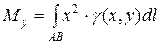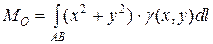Робота змінної сили. Нехай матеріальна точка М 
переходить вздовж кривої L із положення A у положення B , причому під час руху на точку M діє сила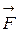 
, напрямок і величина якої змінюються разом із положенням точки M . Знайдемо роботу сили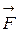 
на переміщенні AB . Для цього виділимо із кривої L елементарну дугу dl 
. Цю дугу можна рахувати прямолінійною і прийняти, що за час руху M вздовж цієї дуги сила 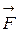не встигає змінитися ні по величині, ні по напрямку. Тоді елементарна робота dA сили на дузі dl може бути знайдена як робота сталої сили на прямолінійному переміщенні, тобто як скалярний добуток сили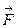 
і вектора переміщення dl. Іншими словами,
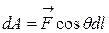
де q - кут між силою 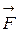і кривою L .
Звідси очевидно, що
.
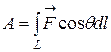Зауважимо, що числове значення сили 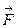та кут q є функціями від координат х, y, z точки М.
Приклад. Визначити масу кривої АВ, якщо задана лінійна густина r = z,
АВ: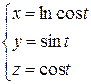 
yA = 0, yB =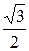 
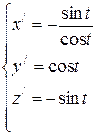tA= 0, tB=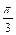 
Розв’язання. Диференціал дуги:
dl =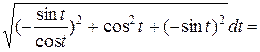 
= 
.
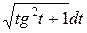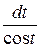m =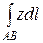 
= 
= 
= 
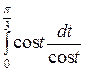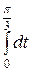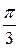(од. маси).
