Этот метод состоит в непосредственном применении таблицы интегралов и их свойств. Если же подынтегральное выражение не является табличным, то необходимо путем тождественных преобразований привести подынтегральную функцию к табличному виду.
Вычислить следующие интегралы.
Пример 1. 
.
Решение.Представим интеграл от алгебраической суммы в виде суммы интегралов (свойство 5), вынося постоянные множители за знаки интегралов (свойство 4) и применяя формулы 2 и 3 таблицы интегралов, получим:
= 
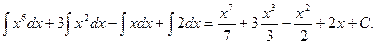
Замечание.Здесь и далее произвольные постоянные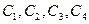 
, входящие по определению в каждый интеграл из суммы, объединяем в одну произвольную постоянную 
.
Пример 2. 
.
Решение.Производим почленное деление, выносим постоянные множители, пользуемся табличными интегралами 3 и 6:
= 
.
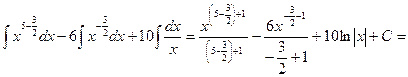
Пример 3. 
.
Решение.Воспользуемся выражением для косинуса половинного угла: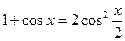 
.
.
Пример 4.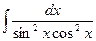 
.
Решение.Воспользуемся основным тригонометрическим равенством: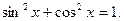 
= 
.
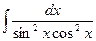