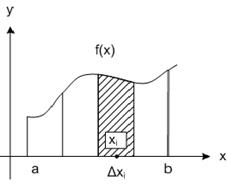
Пусть функция 
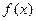непрерывна на отрезке 
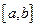. Разобьем отрезок на части 
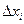и выберем точки 
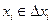. Составим интегральную сумму (сумму Римана) 
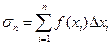. Обозначим 
.
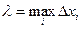Определение. Если существует предел интегральной суммы
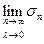, не зависящий от способа разбиения и выбора точек, то он называется (римановым) определенным интегралом функции 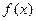на отрезке 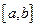и обозначается 
.
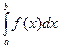Переменная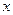 
(переменная интегрирования) представляет собой так называемую «немую переменную», служащую лишь для указания вида функции 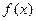, называемой подынтегральной функцией. Немую переменную можно обозначить любой другой буквой. Числа 
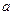и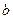 
обычно называют нижним и верхним пределами интеграла. Отрезок 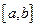называется промежутком интегрирования.
Таким образом,
= .
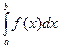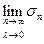