|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Теорема Поста о полнотеДата добавления: 2015-08-31; просмотров: 3038; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| ||||||||||||||||||||||||||||||||||||||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

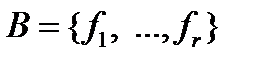
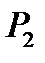 . Спрашивается, как выяснить, будет она полной или нет? Ответ на этот вопрос дает следующая теорема.
. Спрашивается, как выяснить, будет она полной или нет? Ответ на этот вопрос дает следующая теорема.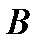 была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов
была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов 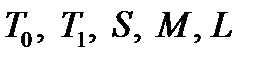 .
.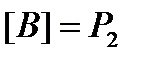 . Допустим, что
. Допустим, что 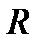 , то есть
, то есть 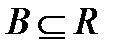 . Тогда в силу свойств замыкания и замкнутости
. Тогда в силу свойств замыкания и замкнутости 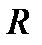 имеем
имеем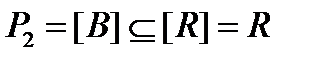 .
.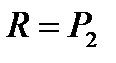 , что не так. Необходимость доказана.
, что не так. Необходимость доказана.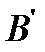 , содержащую не более пяти функций, которая обладает этим свойством. Для этого возьмем в
, содержащую не более пяти функций, которая обладает этим свойством. Для этого возьмем в 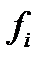 ,
, 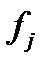 ,
, 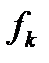 ,
, 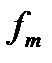 ,
, 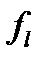 и положим
и положим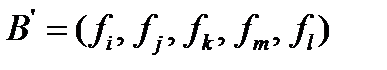 .
.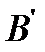 можно построить отрицание и конъюнкцию. Доказательство проведем в два этапа.
можно построить отрицание и конъюнкцию. Доказательство проведем в два этапа.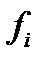 ,
, 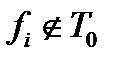 и
и 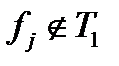 . Построим функции одного аргумента:
. Построим функции одного аргумента: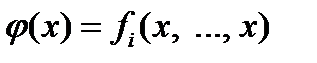 и
и 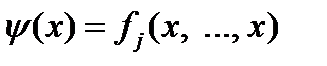 .
.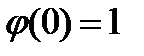 ,
, 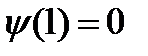 .
.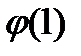 и
и 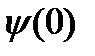 , возможны четыре варианта.
, возможны четыре варианта.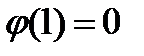 ,
, 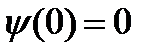 .
.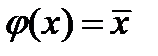 ,
, 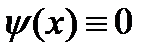 . В результате суперпозиции получаем константу 1:
. В результате суперпозиции получаем константу 1: 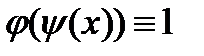 . Таким образом, отрицание и константы построены.
. Таким образом, отрицание и константы построены.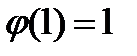 ,
, 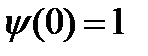 .
.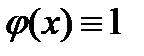 ,
, 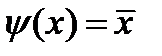 . Строим
. Строим 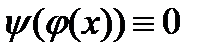 , и первый этап закончен.
, и первый этап закончен.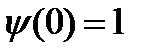 .
.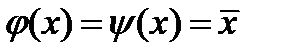 . Воспользуемся функцией
. Воспользуемся функцией 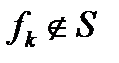 . Для этой функции найдется пара противоположных наборов
. Для этой функции найдется пара противоположных наборов 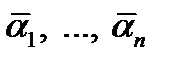 и
и 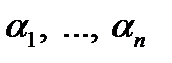 , на которых
, на которых 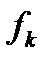 принимает одно и то же значение, так как
принимает одно и то же значение, так как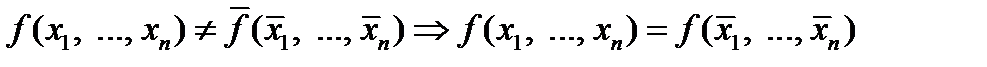 .
.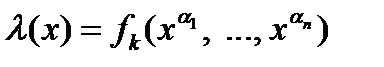 , в которой на место
, в которой на место 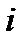 -го аргумента
-го аргумента 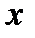 , если
, если 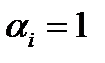 , или
, или 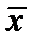 , если
, если 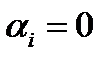 . Тогда
. Тогда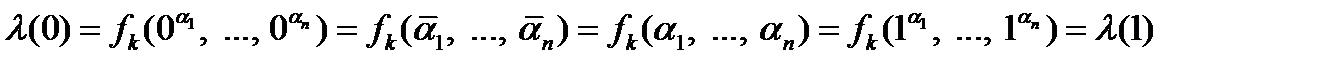 .
.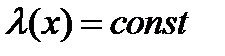 . С помощью отрицания построим другую константу.
. С помощью отрицания построим другую константу.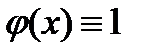 ,
, 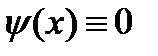 . Воспользуемся немонотонной функцией
. Воспользуемся немонотонной функцией 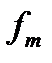 . По лемме 4 из
. По лемме 4 из 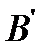 можно построить конъюнкцию. При этом будем использовать построенные на первом этапе константы и отрицание. Воспользуемся нелинейной функцией
можно построить конъюнкцию. При этом будем использовать построенные на первом этапе константы и отрицание. Воспользуемся нелинейной функцией 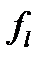 . Подставим в нее константы и построим нелинейную функцию от двух аргументов, что возможно по лемме 6:
. Подставим в нее константы и построим нелинейную функцию от двух аргументов, что возможно по лемме 6: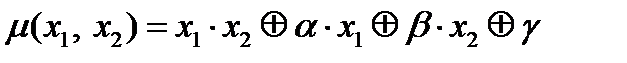 .
.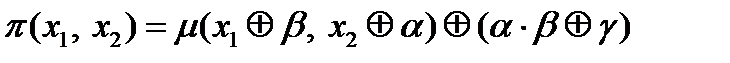 . Для построения функции
. Для построения функции 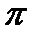 нужно только отрицание, поскольку прибавление двоичной константы либо ничего не изменяет, если она равна 0, либо меняет переменную на ее отрицание. Например, при
нужно только отрицание, поскольку прибавление двоичной константы либо ничего не изменяет, если она равна 0, либо меняет переменную на ее отрицание. Например, при 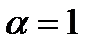 ,
, 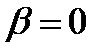 ,
, 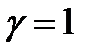
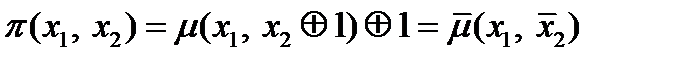 .
.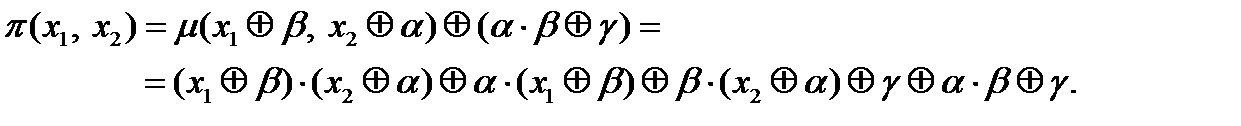
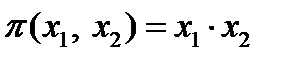 . Таким образом, конъюнкция построена из функций системы
. Таким образом, конъюнкция построена из функций системы 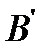 .
.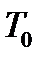 ,
, 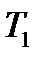 ,
, 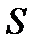 ,
, 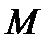 и
и 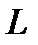 . Например, для системы функций
. Например, для системы функций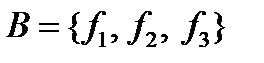 , где
, где 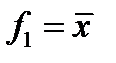 ,
, 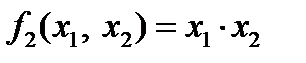 ,
, 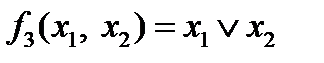
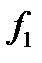
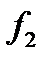
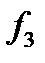
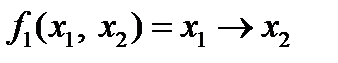 имеет следующую таблицу истинности:
имеет следующую таблицу истинности: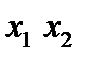
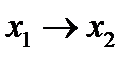
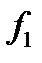 не сохраняет 0, несамодвойственна, немонотонна. Кроме того,
не сохраняет 0, несамодвойственна, немонотонна. Кроме того, 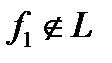 , так как
, так как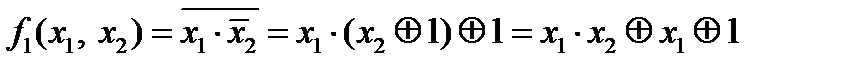 .
.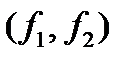 , где
, где 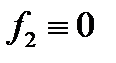 . Построим отрицание и конъюнкцию:
. Построим отрицание и конъюнкцию: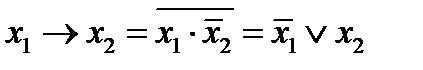 , при
, при 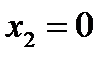 и
и 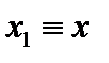 имеем
имеем 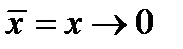 ;
;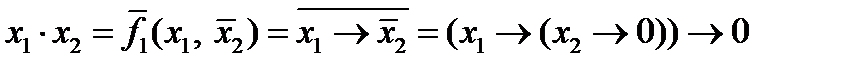 .
.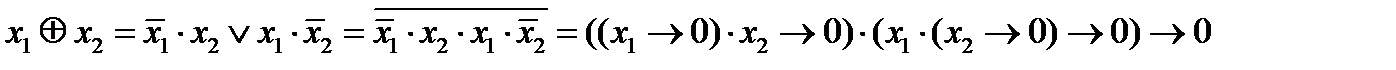 .
.