Обозначим через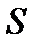 
класс всех самодвойственных функций из 
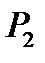, то есть таких, что 
.
Как и выше, нетрудно проверить, что добавление равных функций не выводит за пределы класса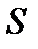 
:
.
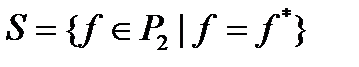Очевидно, что самодвойственными будут функции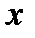 
, 
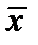. Менее тривиальным примером является функция 
:
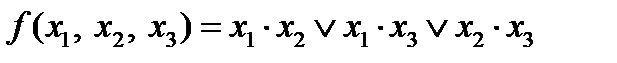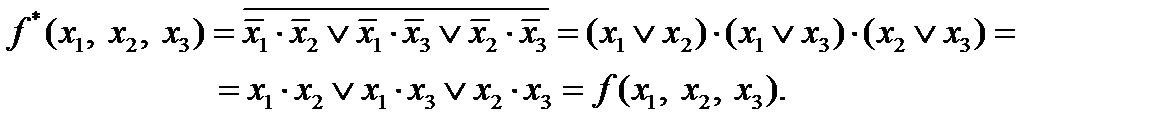
Для самодвойственной функции имеет место тождество
.
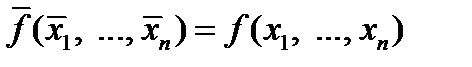Другими словами, на противоположных наборах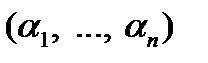 
и 
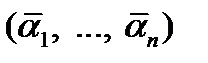самодвойственная функция принимает противоположные значения. Отсюда следует, что самодвойственная функция определяется своими значениями на первой половине строк таблицы истинности. Поэтому число самодвойственных функций 
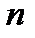переменных равно 
.
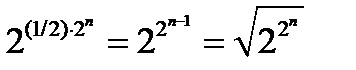Докажем, что класс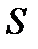 
замкнут, то есть, что суперпозиция самодвойственных функций является самодвойственной функцией. Для этого достаточно показать, что функция
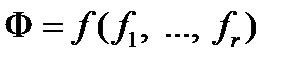
является самодвойственной, если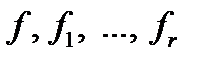 
самодвойственны. Последнее устанавливается непосредственно:
.
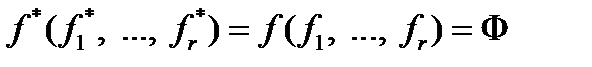Докажем теперь лемму о несамодвойственной функции.
Лемма 2. Если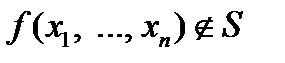 
, то из нее путем подстановки функци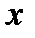й и 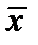можно получить несамодвойственную функцию одного переменного, то есть константу.
Доказательство. Так как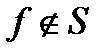 
, то найдется набор 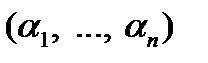такой, что
.
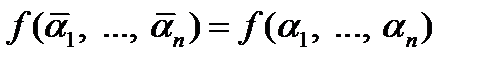Рассмотрим функции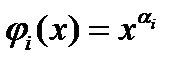 
( 
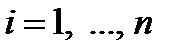) и положим
.
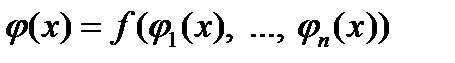Тогда
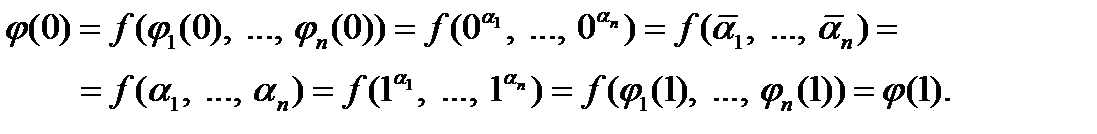
Лемма доказана.
Например, функция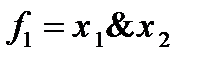 
несамодвойственна, так как 
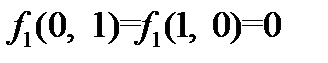. Аналогично для функции 
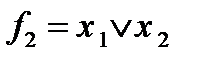имеем: 
.
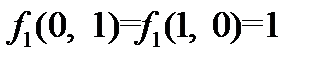