Некоторые классы интегрируемых функций

1. Интегрируемость непрерывных функций.

Теорема 1.Если функция f(x) определена и непрерывна на [a;b] (a<b), то f интегрируема на [a;b].

Доказательство.

Т.к. f непрерывна на [a;b], то она ограничена на нём и равномерно непрерывна на нём (теорема Кантора). Возьмём произвольное разбиение отрезка [a;b] и составим разность , где . Т.к. f непрерывна на [x_k-1;x_k], то m_k является наименьшим, а M_k-наибольшим значением f на [x_k-1;x_k], т.е. существуют x_k′ и x_k″, такие, что f(x_k′)=m_k, f(x_k″)=M_k. Следовательно, . (1)

Выберем произвольное ε>0. Т.к. f равномерно непрерывна на [a;b], то для выбранного ε>0 существует δ>0, такое, что "x′, x″ [a;b], удовлетворяющих условию |x′-x″|<δ, выполнено, |f(x″)-f(x′)|< .

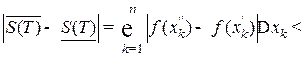
Пусть Т- такое, что λ<δ. Тогда |x_k″-x_k′|≤|x_k-1;x_k|<∆x_k=λ<δ и, следовательно, выполняется неравенство |f(x_k″)-f(x_k′)|< . Тогда из (1) следует, что

₌ .

Получили, что для любого разбиения Т, такого, что λ<δ выполнено . Следовательно, . Значит, согласно критерию интегрируемости, функция f интегрируема на [a;b]

2. Интегрируемость монотонной функции.

Теорема 2.Если функция f(x) определена и монотонна на [a;b], то она интегрируема на [a;b].

Доказательство.

Пусть f(x)-монотонно возрастает на [a;b]. Выберем произвольное разбиение отрезка [a;b]. Т.к. f возрастает, то m_k=f(x_k-1), M_k=f(x_k); M_k>m_k для любого , f(x_k)>f(x_k-1). Пусть ε-произвольное положительное число. Выберем 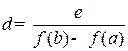. Пусть Т- такое, что λ<δ, тогда

.

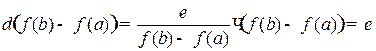Получили, что "ε>0 $δ>0, такое, что для любого разбиения Т: λ<δ выполнено . Это значит, что . Следовательно, f интегрируема на [a;b]

3. Интегрируемость функций, имеющих конечное число точек разрыва.

Теорема 3. Если функция f(x) определена, ограничена на [a;b] и имеет конечное число точек разрыва, то она интегрируема на [a;b].

Определение.Функция f называется кусочно непрерывной на [a;b], если она непрерывна на [a;b], кроме конечного числа точек разрыва, и притом только первого рода.

Следствие.Если функция f кусочно непрерывна на [a;b], то она интегрируема на [a;b].

Лемма.Пусть f и g определены на [a;b] и f(x)=g(x) "x (a;b). Тогда, если f интегрируема на [a;b], то и g интегрируема на [a;b] и

.

Лемма утверждает, что если f интегрируема на [a;b], то её интегрируемость и величина определённого интеграла не изменится, если изменить значения функции f на концах отрезка и также в любом конечном числе точек отрезка.

Множество всех функций, интегрируемых по Риману на [a;b] обозначают R[a;b]. Т. о., f R[a;b] тогда и только тогда, когда f R(a;b).

Расширим понятие определённого интеграла. Будем считать по определению, что .