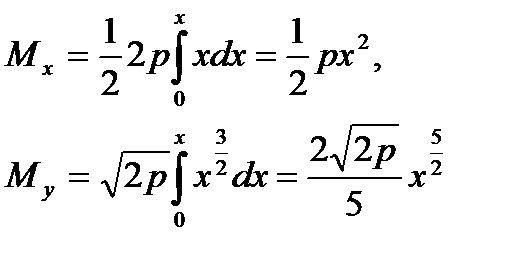Статический моментом относительно оси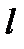 
материальной точки А, имеющей массу m и отстоящей от оси l на расстоянии d,называется величина
Статическим моментом относительно оси l системы n материальных точек с массами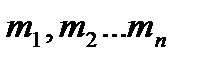 
,лежащих в одной плоскости с осью и удаленных от неё на расстояния d1,d2,…..dn называется сумма
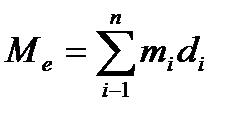
Причем расстояние точек, лежащих по одну сторону оси L,берутся со знаком плюс (+),а по другую –со знаком минус(+). Если массы непрерывно заполняют линию или фигуру плоскости XOY ,то статические моменты Mx и My относительно координатных осей ОХ и ОY выражаются соответствующими интегралами. Для случая геометрических фигур плотность считается равной единице.
1)Для кривой x=x(s) y=y(s) где параметр s есть длина дуги имеем
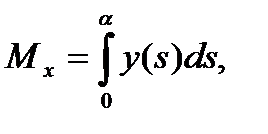
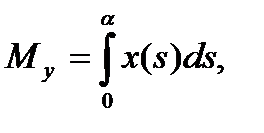
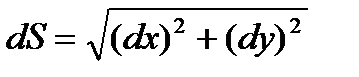-дифференциал дуги.
2)Для плоской фигуры ,ограниченной кривой y=y(x),осью OX и двумя вертикалями x=a и x=b имеем:
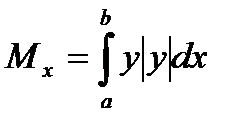
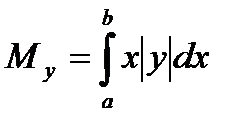
7.6.1. Найти статические моменты Mx и My треугольника ограниченного прямыми x+y=a , x=0 , y=0 (плотность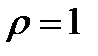 
)
Решение.
Здесь y=a-x
Применяя формулы получим
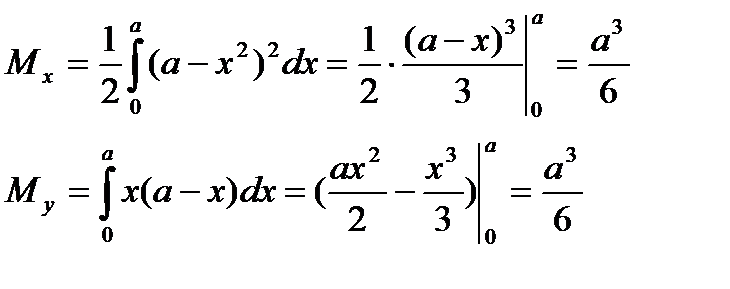
Равенство моментов можно было установить и из соображения симметрии.
7.6.2.Найти статические моменты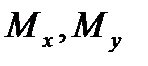 
и фигуры ,ограниченной параболой 
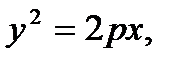осью 
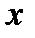и ординатой ,соответствующей абсциссе 
.
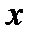Решение: Так как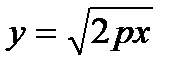 
,то
