Если кривая задана параметрическим уравнениями
,
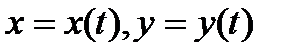
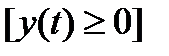То площадь поверхности, образованной вращением вокруг оси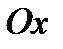 
дуги этой кривой, вычисляется по формуле
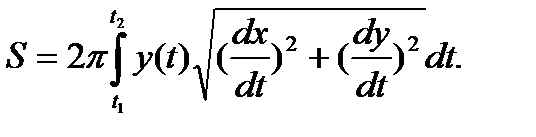
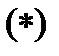
где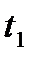 
и 
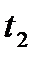
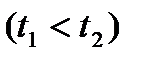-значение параметра 
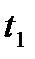соответствующее концам дуги.
Если кривая задана уравнением вида
,
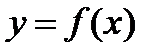То вместо формулы 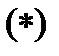получим
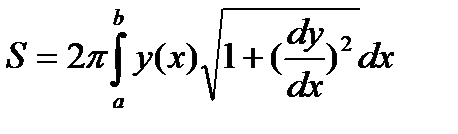
Где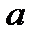 
и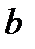 
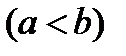- абсциссы начала и конца дуги.
6.5.1.Найти площадь поверхности, образованной вращением вокруг оси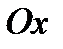 
дуги синусоиды 
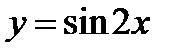от 
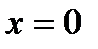до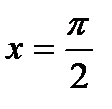 
Решение. Находим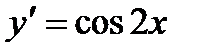 
,тогда
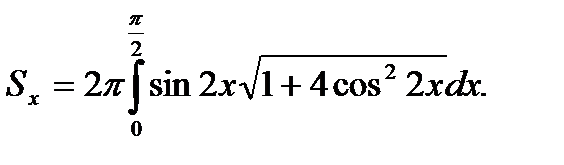
Сделаем замену переменной
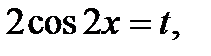
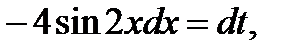
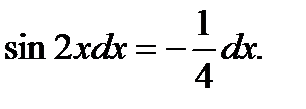
Найдём пределы интегрирования по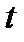 
:
если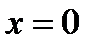 
,то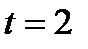 
если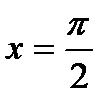 
, то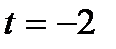 
Таким образом
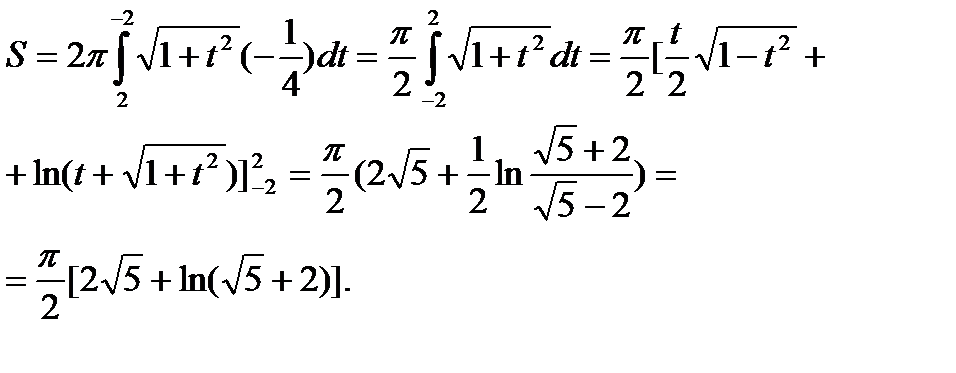
6.5.2.Найти площадь поверхности, образованной вращением вокруг оси Ох дуги кубической параболы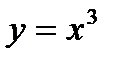 
заключённой между прямым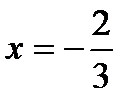и 
и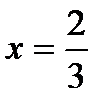 
Решение. Построив дугу параболы между точками А и В где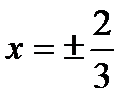 
,
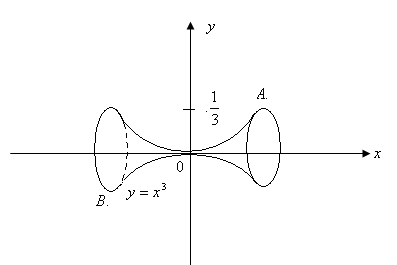
замечаем, что образуемая поверхность вращения этой дуги вокруг оси Ох состоит из двух одинаковых частей.
Поэтому согласно формуле имеем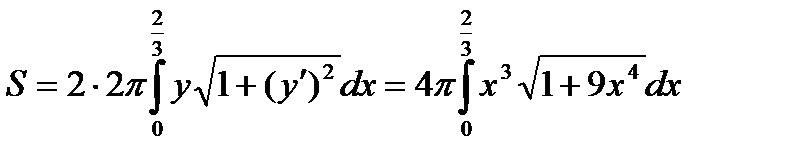 
Для вычисления интеграла полагаем
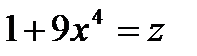
Тогда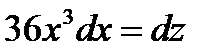 
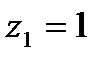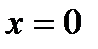
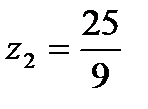при 
при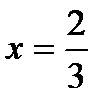 
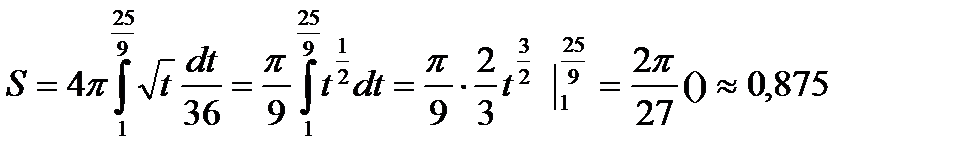
6.5.3.Найти площадь поверхности, образованной вращением вокруг оси абсцисс астроиды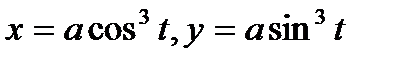 
Решение
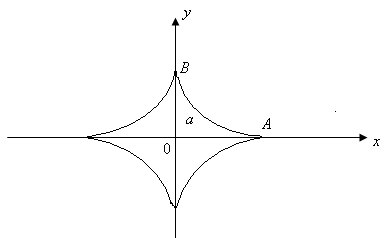
Составим подынтегральные выражения в соответствии с формулой
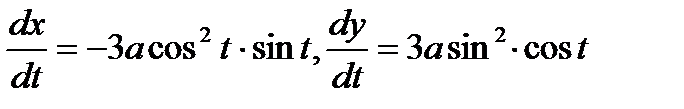
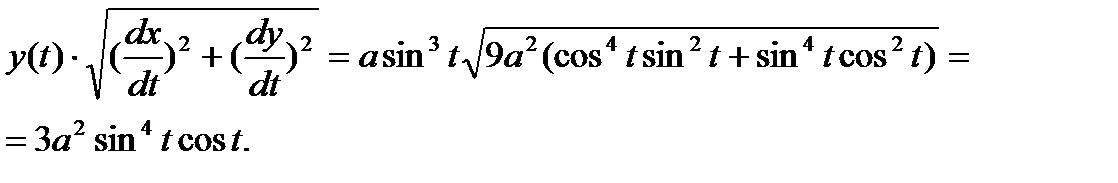Изменения параметра е от t=0 до 
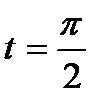соответствует движение точки по астроиде от А до В. Дуга АВ при вращение оси Ох половину искомой площади, поэтому
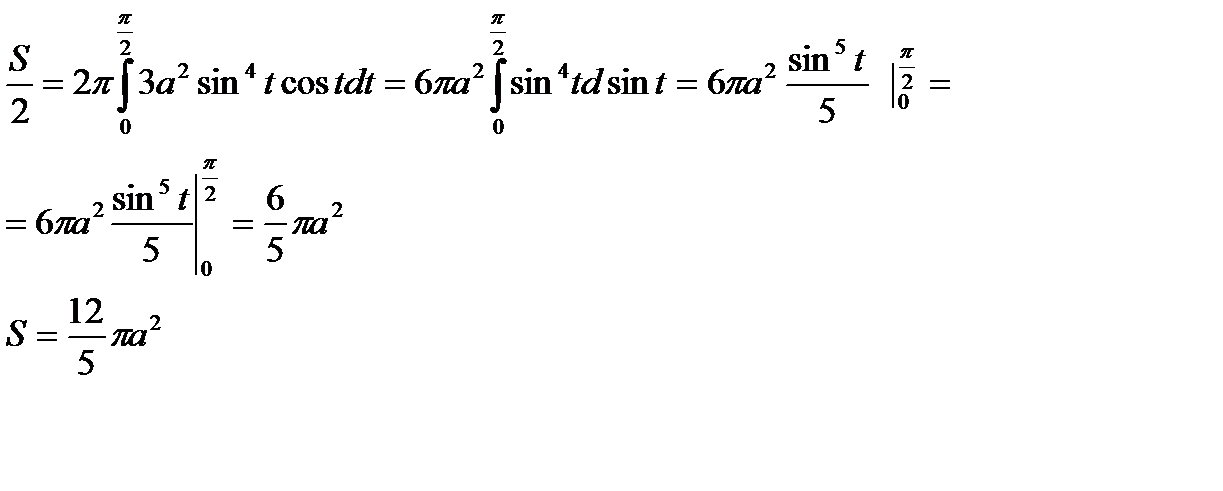
Приложения определенных интегралов к решению задач физики.
