|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Интегрирование по частям в определенном интеграле.Дата добавления: 2015-08-31; просмотров: 1483; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

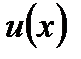 и
и 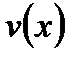 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 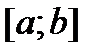 . Тогда справедлива формула:
. Тогда справедлива формула: 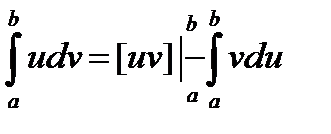 -формула интегрирования по частям для определенного интеграла.
-формула интегрирования по частям для определенного интеграла.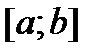 имеем;
имеем; 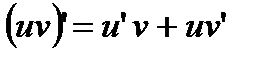 Интегрируем обе части этого тождества в пределах от a до b:
Интегрируем обе части этого тождества в пределах от a до b: 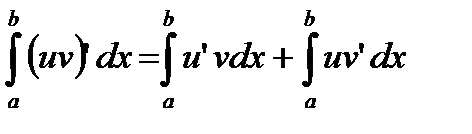 ; или
; или 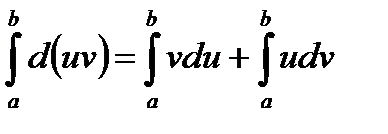 ; откуда имеем
; откуда имеем 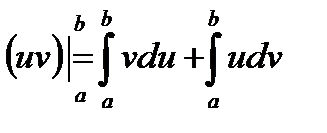 ;
; 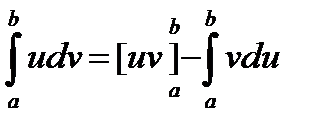 . Что и требовалось доказать.
. Что и требовалось доказать.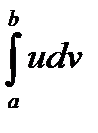 к вычислению интеграла
к вычислению интеграла 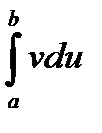 , который в ряде случаев может оказаться более простым, чем первоначальный. Практика применения этой формулы почти такая же, что и для соответствующей формулы в теории неопределенных интегралов.
, который в ряде случаев может оказаться более простым, чем первоначальный. Практика применения этой формулы почти такая же, что и для соответствующей формулы в теории неопределенных интегралов.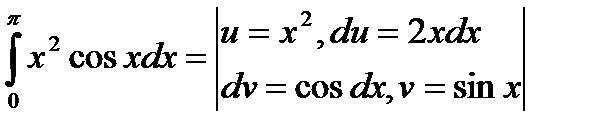
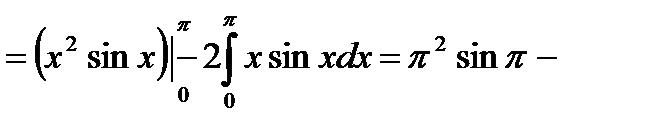
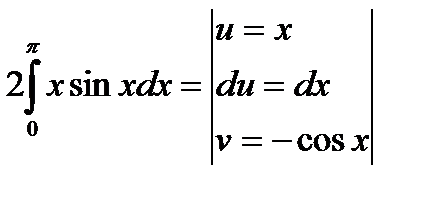
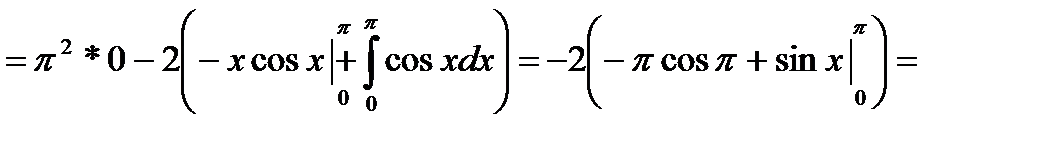
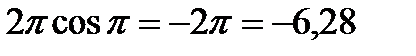 Часто здесь бывает удобно применить, как и в случае вычисления неопределенного интеграла, замену переменной путем введения вместо старой переменной новой переменной t, связанной со старой соотношением
Часто здесь бывает удобно применить, как и в случае вычисления неопределенного интеграла, замену переменной путем введения вместо старой переменной новой переменной t, связанной со старой соотношением 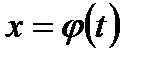 .
. , положив
, положив  определена и непрерывна на отрезке
определена и непрерывна на отрезке 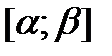
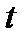 на
на 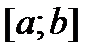 . При этом
. При этом 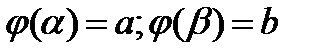
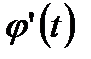
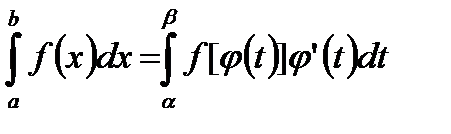 (4.1)
(4.1)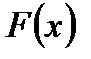 -какая-либо первообразная для функции
-какая-либо первообразная для функции 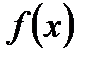 на
на 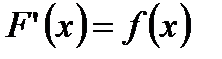 . Тогда по формуле Ньютона-Лейбница имеем:
. Тогда по формуле Ньютона-Лейбница имеем: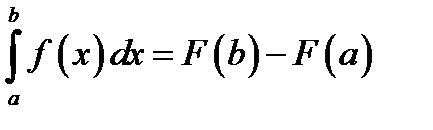 (4.2)
(4.2) переменной
переменной  . Эта функция сложная.
. Эта функция сложная.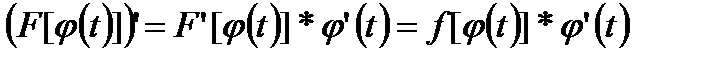
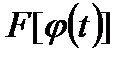 является первообразной для
является первообразной для 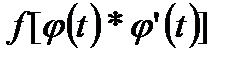 на отрезке
на отрезке 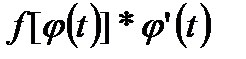 непрерывна на
непрерывна на 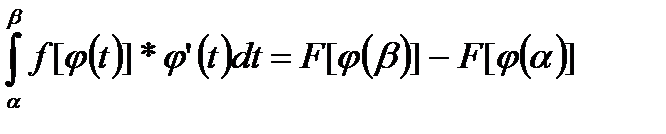 но по условию
но по условию 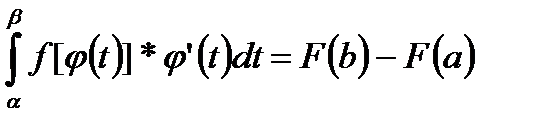 . (3)
. (3)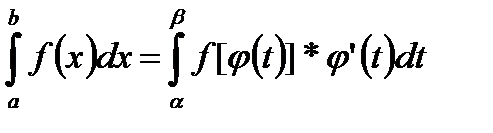
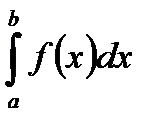 к вычислению интеграла
к вычислению интеграла 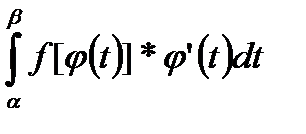 .
.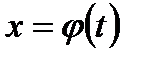 стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный. и
и  нового интеграла определяются из уравнений:
нового интеграла определяются из уравнений: 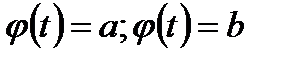 каждое из этих уравнений может иметь несколько корней, при этом за
каждое из этих уравнений может иметь несколько корней, при этом за 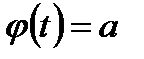 , а за
, а за 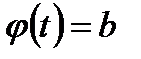 , лишь бы выполнялись условия 2) и 3), при которых установлена формула (4.1).
, лишь бы выполнялись условия 2) и 3), при которых установлена формула (4.1).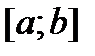 . Поэтому на практике замену переменной часто осуществляют с помощью монотонных функций, тем более что при применении формулы (4.1) оперировать с такими функциями проще, чем с немонотонными.
. Поэтому на практике замену переменной часто осуществляют с помощью монотонных функций, тем более что при применении формулы (4.1) оперировать с такими функциями проще, чем с немонотонными.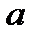 и
и 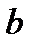 , то она не может служить для выполнения замены переменной в этом интеграле. Так, например, нельзя, очевидно, преобразовать в интеграле
, то она не может служить для выполнения замены переменной в этом интеграле. Так, например, нельзя, очевидно, преобразовать в интеграле 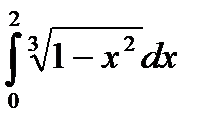 подынтегральную функцию с помощью подстановки:
подынтегральную функцию с помощью подстановки: 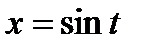 .
.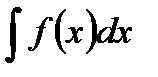 с помощью замены переменной
с помощью замены переменной 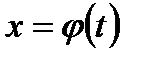 , мы должны были, найдя
, мы должны были, найдя 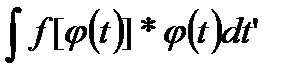 , ещё вернуться затем к прежней переменной
, ещё вернуться затем к прежней переменной 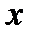 .
.