На практике часто встречается гипербола с равными полуосями.
Если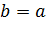 
, то каноническое уравнение 
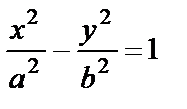заметно упрощается:
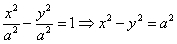
А вместе с ним упрощаются и уравнения асимптот:
Прямые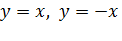 
пересекаются под прямым углом и делят координатную плоскость на 4 одинаковые части, в двух из которых находятся ветви кривой.
Так как 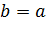, то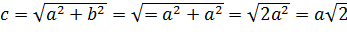 
,
следовательно, эксцентриситет любой равносторонней гиперболы равен:
.
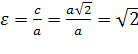Упражнения:
1. Построить гиперболу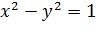 
и найти её фокусы.
2. Тело движется так, что в любой момент времени находится к точке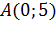 
ближе на три единицы масштаба, чем к точке 
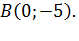Найти уравнение и построить эскиз траектории движения тела.
3. Составить уравнения прямых, проходящих через точку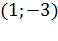 
и параллельных ассимптотам гиперболы.
4. Найти острый угол между ассимптотами гиперболы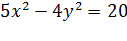 
.
Указание к решению задачи: использовать формулу для нахождения угла между прямыми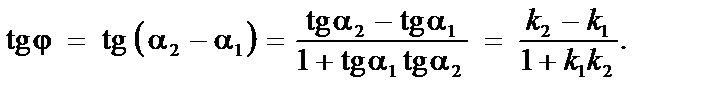 
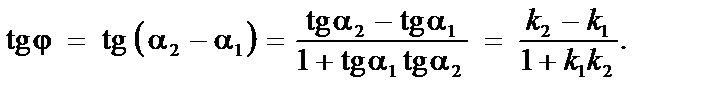
5. Найти эксцентриситет гиперболы, если известно, что угол между её ассимптотами равен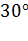 
.
6. Составить уравнение гиперболы, эксцентриситет которой равен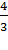 
, имеющей общие фокусы с эллипсом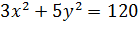 
Указание к решению задачи: учесть, что фокусы расположены на той же оси, что и у эллипса.
Ответ: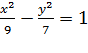 
.
Литература:
1. Лисичкин В.Т.,Соловейчик И.Л. Математика: Учеб. Пособие для техникумов. – М.:Высш.шк.,1991. – 480 с.: ил., стор. 156-157.
2. Письменный Д.Т. Конспект лекцій по высшей математике: полный курс. – 4 изд. – М.: Айрис- Пресс, 2006. – 608 с.: ил. - §11, п.4.
