Перед решением этих примеров следует изучить лекции 4 и 5.
1) По теореме 6, стр. 18, при 
многочлен эквивалентен своему одночлену с наивысшей степенью. Так как во всех вариантах 
и 
, то 
~ 
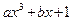и
~ 
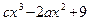. По теореме 7, стр. 18, числитель и знаменатель можно заменить на эквивалентные им функции. Имеем:
.
2) Из цепочки эквивалентностей (8), стр.17, следует, что при 
~ 
, а значит 
~ 
(это легко вытекает из определения 11, стр.17). Из той же цепочки эквивалентностей получаем, что 
~ 
. Заменяя числитель и знаменатель эквивалентными им функциями, получаем:
.
Отметим, что проведенные рассуждения были возможны, так как во всех вариантах параметры a, b и c отличны от нуля.
3) Решение этого примера совершенно аналогично решению примера 13, стр. 20. Имеем: при 
~ 
~ 
~ 
, 
~ 
~ 
. Поэтому
.
4) Для решения этого примера (который совершенно аналогичен примеру 14, стр. 21) следует применить правило Лопиталя (см. теорему 9 на стр. 20-21). Имеем:
.
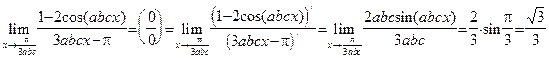5) Перед решением этого примера следует просмотреть пример 19 на стр. 22. Обозначим 
и прологарифмируем данное равенство. Получаем:
.
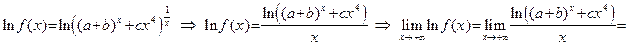
Применяя еще пять раз правило Лопиталя, и в результате получим:
.
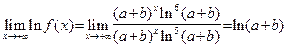Перейдем теперь от логарифма к самой функции:
.
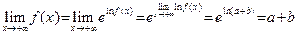Заметим, что вместо пятикратного применения правила Лопиталя можно было применить эквивалентность (именно так сделано в примере 19).
Задача №3
Провести полное исследование функции 
и построить ее график.
