Определение 6.Прямая  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 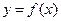 , если
, если  - БМФ при
- БМФ при  , т.е.
, т.е.  .
.
Теорема 6.Функция  имеет наклонную асимптоту тогда и только тогда, когда
имеет наклонную асимптоту тогда и только тогда, когда  , а
, а  .
.
Доказательство:
Необходимость. Пусть функция  имеет наклонную асимптоту. Тогда по определению
имеет наклонную асимптоту. Тогда по определению  . Разделим обе части равенства на
. Разделим обе части равенства на  и получим:
и получим:  .
.
Перейдем к пределу при 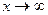 :
:
 . Следовательно,
. Следовательно, 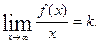
Рассмотрим  . Перейдем к пределу:
. Перейдем к пределу:
 .
.
Достаточность. Пусть  ,
,  . Тогда рассмотрим функцию
. Тогда рассмотрим функцию  в окрестности бесконечно удаленной точки
в окрестности бесконечно удаленной точки  :
:

 где
где 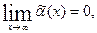
 =>
=> 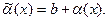
 . ■
. ■
Замечание.Если 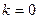 , то говорят, что функция имеет горизонтальную асимптоту
, то говорят, что функция имеет горизонтальную асимптоту  .
.
Замечание.Если на отрезке  функция имеет разрыв второго рода в точке
функция имеет разрыв второго рода в точке  , то прямая
, то прямая  называется вертикальной асимптотой.
называется вертикальной асимптотой.