(рисунок)
Так как 
, то дифференциал функции равен 
. Таким образом, 
.
Физический смысл дифференциала
Пусть тело движется по закону 
. Тогда дифференциалом перемещения 
является то приращение расстояния за промежуток времени 
, пройденное со скоростью 
в промежутке 
. Таким образом, 
.
Инвариантность дифференциала функции
Если функция 
является сложной, то ее дифференциал равен 
. Тогда 
или 
.
Замечание.С дифференциалами обращаются также как и с производными, поэтому для дифференциала справедливы те же правила дифференцирования. На практике дифференциал применяют для приближенных вычислений:
, 
, т.е. .
Пример.Вычислим 
. Для этого рассмотрим функцию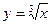 
в точке 
. Приращение 
, тогда 
, 
, 
.
п. 5 Производные и дифференциалы высших порядков
Определение 1.Пусть функция 
имеет производную 
порядка. Тогда производной 
-го порядка называется 
.
Пример. 
.
Для нахождения производной произведения -го порядка пользуются аналогом бинома Ньютона:
; 
.
Заметим, что 
, тогда 
.
Определение 2. Дифференциалом -го порядка называется
.
В частности,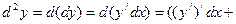 
.
