Пусть 
и 
- положительные числовые ряды. Если 
, то из сходимости ряда следует сходимость . Если 
, то из расходимости числового ряда следует расходимость .
Следствие.
Если и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.
Исследуем ряд 
на сходимость с помощью второго признака сравнения. В качестве ряда возьмем сходящийся ряд 
. Найдем предел отношения k-ых членов числовых рядов:
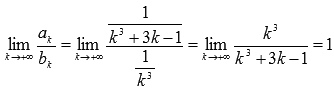
Таким образом, по второму признаку сравнения из сходимости числового ряда следует сходимость исходного ряда.
