Пусть n > 1. Как мы знаем, дифференциальное уравнение n-го порядка имеет вид
(1)
Если уравнение (1) имеет вид
(1'),
то уравнение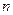 
- го порядка (1') называется разрешенным относительно 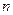-ой производной. Функция 
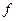в правой части уравнения (1') есть функция 
переменного. Общее решение уравнения (1') имеет вид
,
где 
– постоянные.
Общим интегралом уравнения (1) или (1') называется соотношение 
, задающее неявно решение уравнений (1) или (1'), соответственно.
Теорема 1. Пусть правая часть 
уравнения (1'), рассматриваемая как функция переменного 
, непрерывна, и имеет в некоторой окрестности точки 
непрерывные частные производные 
. Тогда на некотором интервале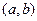 
, содержащем точку 
, найдется 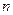раз непрерывно дифференцируемое решение 
уравнения (1'), удовлетворяющее условиям
. (2)
При этом решение дифференциального уравнения (1'), удовлетворяющее условиям (2), единственно.
Условия (2) называются начальными. Задача отыскания решения дифференциального уравнения (1'), удовлетворяющего начальным условиям, называется задачей Кoши.
