ТЕОРЕМА 6.1. Пусть 
. Тогда
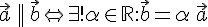
Доказательство необходимости. Существование докажем конструктивно, т.е. укажем число удовлетворяющее
условиям теоремы. Положим
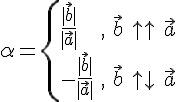
Легко проверить, что векторы 
и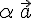 
имеют одинаковые длины и направления. Следовательно, 
.
Докажем теперь единственность. Пусть существует еще число 
такое, что 
. Тогда имеем равенство
так как .
Доказательство достаточности. Непосредственно следует из определения произведения вектора на число.
· Мой профиль
· Мои курсы
· Геометрия мат
· Теор алг
· ИКТ_обр_мат
· Векторы
· Участники
· 
Настройки
· Внешние блоги
· ПРШМЗ
· ТМОИ (3к-мат)
